[TOC]
个性化推荐算法实践第10章基于深度学习的排序模型WideAndDeep
欢迎来到本次个性化推荐算法实战课程,本课程是有问答专区,如果你有问题可以在问答专区提问,我会在每天固定时间解答,课程结合问答专区能够让您更快的掌握知识。
开始本章节的课程之前,我们首先来回顾一下上一章节的内容,上一章节我们重点讲述了树模型GBDT的数学原理,以及在测试数据集上代码实战了GBDT模型的训练,并且介绍了GBDT与逻辑回归的混合模型,那么本章节我们将重点介绍深度学习,在点击率预估方面的实战,分别介绍WD模型的数学原理,以及在测试数据集上代码实战WD模型的训练。
背景介绍之深度学习
DNN网络结构与数学原理
WD(wide and deep)网络结构与数学原理
下面我们首先来看一下本章节的内容大纲。1、背景知识介绍之深度学习,由于本章节所介绍的内容与之前我们所学习的浅层模型有较大的不同,所以我们首先介绍一下背景知识,什么是深度学习?2、DNN网络结构与数学原理,介绍完什么是深度学习,我们便选取一种具有代表性的网络DNN,来从它的数学原理如何进行参数学习来详解一下。3、WD网络结构与数学原理,WD模型便是我们所说的,使用深度学习来完成点击率预估实战所采用的模型,wd模型实际上是DNN与逻辑回归的混合模型,但是与之前我们所介绍过的GBDT与逻辑回归的混合模型不同,WD呢是联合训练的,所以我们要学习一下它的网络结构,并且详细的了解一下它的数学原理是如何做到联合训练的。
一、背景介绍之什么是深度学习
1.1什么是神经元?
下面开始本小节的内容,本小节将重点介绍背景知识,什么是深度学习?深度学习,实际上是利用神经网络学习出一种非线性函数,该函数的输入是我们从训练数据中提取的特征,该函数的输出是训练数据所对应的label,那么说到这里,问题的核心就变成了什么是神经网络,在介绍神经网络之前,我们首先介绍一下它的组成成分,神经元,什么是神经元呢?下面来看一下,这里所说的神经元呢,实际上是指的是人工神经元,与我们生物上神经元的概念呢有所不同。但是呢,我们通过这个网络结构呢,实际上能够联想一下我们生物上的神经元,与该结构有极大的相似性。
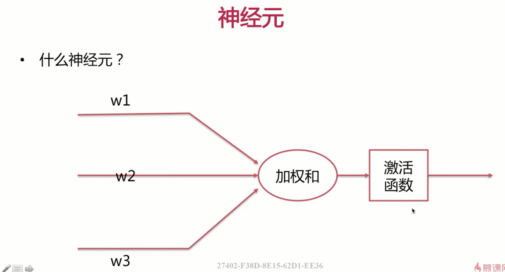
下面我们来看一下该结构,这里有几路输入,每一路输入了对应的输入的参数。也就是说我们最终的加权和是什么呢?我这里简单的写一下,加权和=$w_1x_1+w_2x_2+w_3x_3+…+w_nx_n$。加权和之后呢,还要做一下激活函数,这里的激活函数呢,主要是去线性化。常用的激活函数呢,我们在介绍逻辑回归模型的时候,也曾介绍过一种阶跃函数,大家应该还记得。这里的整体的网络结构呢与我们的逻辑回归模型的有一定的相似性。
1.2激活函数
那么下面我们来看一下常用的激活函数有哪一些呢?
1.2.1阶跃函数 sigmod
第1种呢是我们比较熟悉的阶跃函数,该函数我们曾在逻辑回归里介绍过,该函数的取值范围呢是[0~1],在x等于0时的函数值是0.5,他有一个特点那便是在x大于0的时候,很快函数值就趋向于1。x小于0的时候,函数值非常快的就趋向于0。
1.2.2双曲正切
第2种呢,是双曲正切,该函数的图像呢与阶跃函数几乎是一样的,只不过呢,它的取值范围呢是[-1,+1],而且呢,该函数在取值为中间值变为最大值,以及取值为中间值变为最小值的速度呢,要比阶跃函数要快一些。
1.2.3修正线性单元
第3种,修正线性单元,当输入大于零时,该函数的输出的是输入的本身,当输入小于零时,该函数的输出呢是0。在神经网络的参数学习中呢,如果我们采用之前讲述过的随机梯度下降的方法,修正线性单元函数能够更快的达到收敛。
1.3 什么是神经网络?
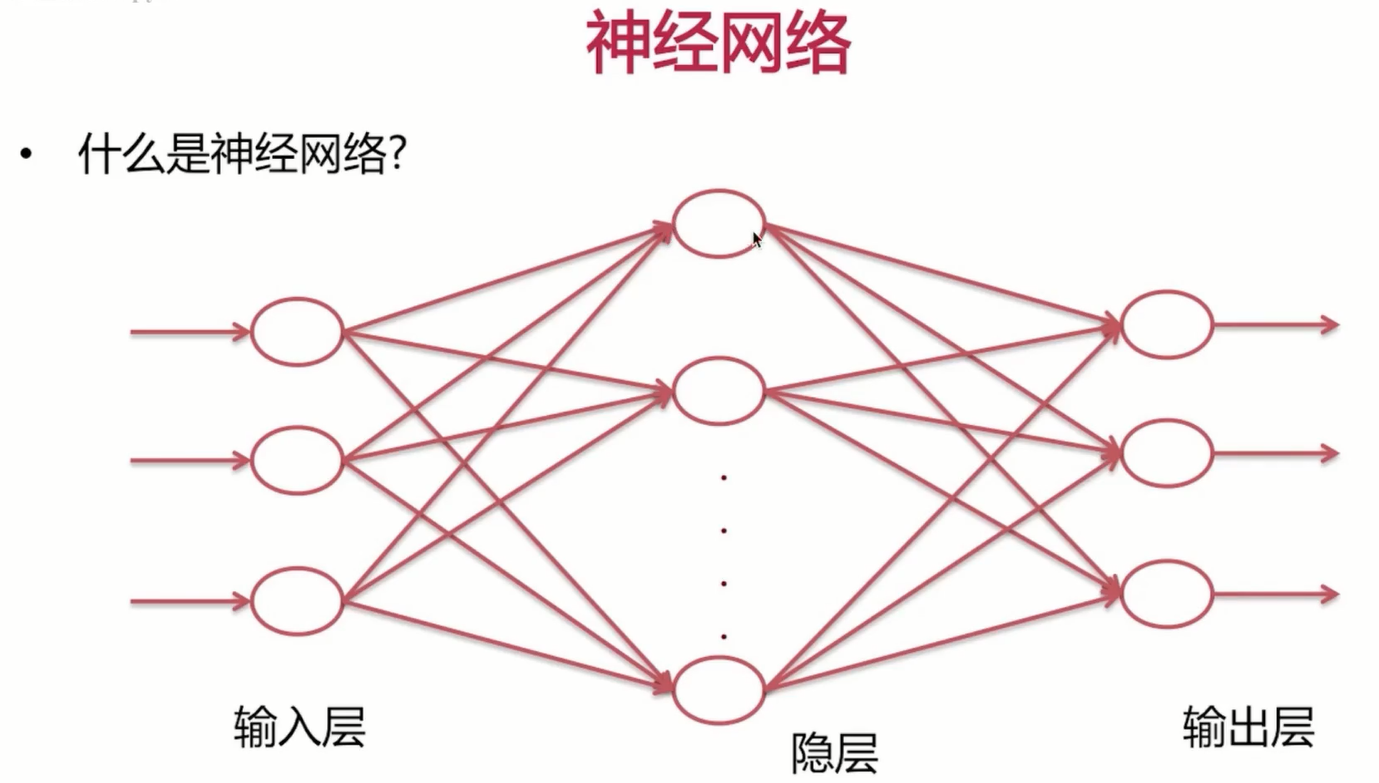
好了介绍完了激活函数,下面我们来学习一下什么是神经网络。神经网络呢是由许多神经元组成的,我们先来简单的看一下网络结构,网络结构呢分为输入层,隐层以及输出层。
输出层呢,可以是一个也可以是多个。像我们做点击率预估呢,那便是一个。如果我们做分类呢是多分类的话,显然就是多个。有几个分类呢,也就有几个输出。输入指的是什么呢?输入指的是我们提取的特征,输入层呢,与隐层之间的采用的是全连接,也就是说我这里的隐层1与我输入层的每一个输入,都有参数相连。这里的隐层2呢,对于输入层的每一个输入呢,也都是有参数相连的。这里参数相连去加权求和之后呢,同样需要有激活函数来去线性化。
我们发现如果输入层与隐层不是全连接的话,而是一一连接的话,那么该网络也便回退到了我们之前讲述过的逻辑回归模型。为什么呢?很好理解,如果是一一连接的话,很像我们之前讲述过的w1与x1相乘,w2与x2相乘。
这样全连接呢,实际上相当于我们在逻辑回归模型里所做的特征交叉,但是呢,这里交叉的力度呢,会更强一点。
举个例子,如果我们这里只有三个输入特征,且并非全连接。对该隐层的第1个节点,我们让三个输入特征的前两个与它连接,实际上这就相当于完成了我们之前所做的两维特征的特征交叉。
而这里呢,由于每一个节点与之输入层都是全连接的,所以参数的规模呢要比之前大了非常多。我们来看一下一共有多少个参数呢?比如说我们的输入层一共有三个节点,隐层也是有三个节点,那么隐层的每一个节点,显然啦,与输入层之间的都是全连接,也就是都是三个参数,以及每一个隐层的节点呢,都需要一个偏执,所以这里总的参数呢,是3×3+3=12。而相同情景下逻辑回归的参数呢,只有三个,所以从参数量级上呢,神经网络还是要大很多的。
如果按当时我们训练逻辑回归模型所举的例子,输入特征100多维这里就按100维来算的话,隐层的节点如果有n个。那么这里的总参数便是(100n+n)也就是101n,而我们知道逻辑回归当中的这种情形下只有100个参数,所以呢,总体来讲参数的量级上呢,差了n倍,这个n呢是隐层的节点数目,也就是说隐藏的节点数目越多的话,参数的量级差距越大,神经网络能够学习到的隐含特征的也就越丰富。
1.3深度学习与传统的机器学习有哪些流程的异同呢?
DL DIFFS ML
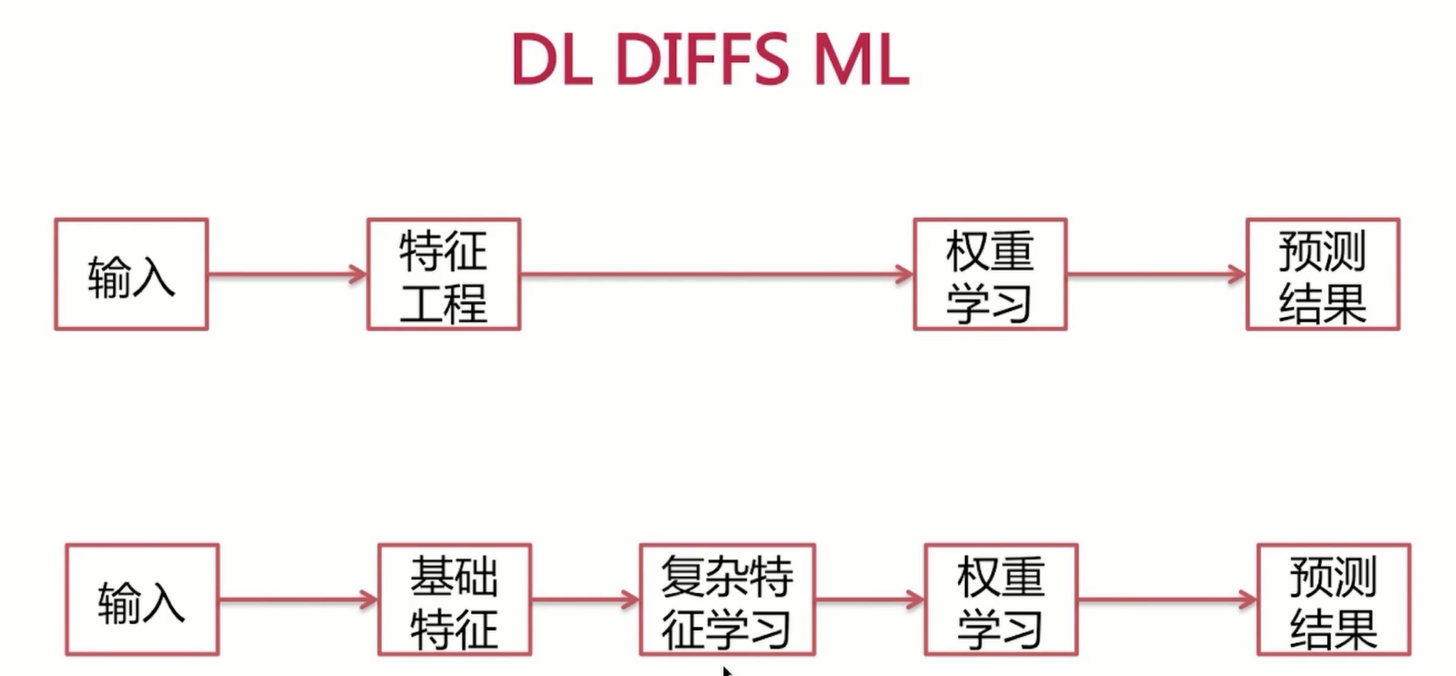
介绍完了神经网络,下面我们来看一下深度学习与传统的机器学习有哪些流程的异同呢?首先呢,我们来看一下传统的机器学习。这里以我们所学习过的逻辑回归模型的训练为例,我们拿到训练数据之后呢,需要做特征工程,这里的特征工程呢,是指我们要挑选相应的特征,我们要做特征的离散化。归一化甚至呢,我们要区分连续特征以及离散特征不同的处理,最终呢,我们还要做特征的交叉等等,我们把特征工程处理好了之后呢,我们便得到了训练样本,训练样本呢,在传入的模型当中呢,去进行权重的学习,也就是参数的学习,最终呢,我们得到模型来完成结果的预测。
但是在深入学习中呢,我们只需要对输入的训练样本呢进行基础特征的抽取,而不再需要做繁琐的特征工程,繁琐的特征工程呢,相当于交由我们模型当中的多维参数来帮我们学习,这里呢,神经网络呢,就学习了这些复杂特征,进而呢在隐层之间呢,我们学习模型的参数,得到模型之后呢,我们便用来预测结果。好了本小节就全部结束了,本小节重点介绍了背景知识之什么是深度学习,下一小节我们将选取一种经典的深度神经网络DNN来介绍它的网络结构与数学原理。
二、DNN网络结构与反向传播算法
2.1DNN网络结构
开始本小节的课程之前,我们首先来回顾一下上一小节的内容,上一小节我们重点介绍的背景知识,什么是深度学习,那么本小节我们叫重点介绍,DNN网络结构以及DNN网络结构参数学习的数学原理,下面开始本小节的内容,下面我们来看一下DNN网络结构,DNN呢,实际上是深度神经网络与我们之前介绍过的,神经网络的结构呢,有相似性,也有不同的地方相似的地方呢。
相似的地方就是这里也分为三个大部分,第1大部分呢便是输入层,这是我们特征。多了的地方,第2大部分呢是隐层是我们基础特征的抽象到高阶特征,然后高阶特征之间参数不停的学习的过程。第3部分呢便是输出层,这里可以是一个节点,像我们在点击率预估问题中呢,便是一个输出,也可以是多个输出,像我们在多分类问题当中呢,便是多个输出。
但是这里与我们之前讲过的神经网络有不同的地方呢,便是我们的隐层呢,这里可以是多层,每一层的节点呢可以变得不同,好了这便是DNN网络结构。当然这里输入层与隐层,隐层与隐层,隐层与输出层之间的也都是全连接。
2.2 DNN模型参数
2.2.1 隐层的层数,每个隐层神经元的个数,以及激活函数
好了,下面让我们来看一下DNN模型当中有哪些重要的参数是值得我们注意的。首先呢,便是隐层的层数,每个隐层神经元的个数,以及激活函数。隐层的层数以及每个隐层神经元的个数呢,决定了网络的参数的量级,这里上一小节呢,我们曾经简单的举例过,三个维度特征的输入以及单隐层,三个隐层节点的话,它的参数呢是3×3+3,那么很明显我们这里可以以此类推,如果隐层与隐层之间的计算方式呢,也是这么计算,模型的参数的量级呢,是由隐层的层数以及每个隐层神经元的个数来决定的。当然了,还与我们输入特征的维度有直接的关系。激活函数的上一小节我们曾经介绍过三种,这里我们说过激活函数呢是决定我们参数收敛的快慢的。
2.2.2 输入输出层的向量维度
输入输出层的向量维度,如果是单维度的输出的话,像我们点击率预估这种问题就需要单维度的输出。如果是多维度的输出,像多分类问题呢,就需要多维度的输出。输入层的向量呢,是我们选定好基础特征之后呢,在完成,像字符串的哈希,然后做一个简单的Embedding或者说是我们这里将连续值呢进行分段离散等等的操作之后呢,我们得到的一个输入层的向量。
2.2.3 不同层之间神经元的连接权重与偏移值B
我们需要学习的参数是什么呢?就是不同层之间神经元的连接权重,这里可能是输入层与隐层,隐层与隐层,隐层与输出层之间的连接权重,以及呢每一个节点上的偏移值,这是我们模型需要学习的参数。
2.3 前向传播
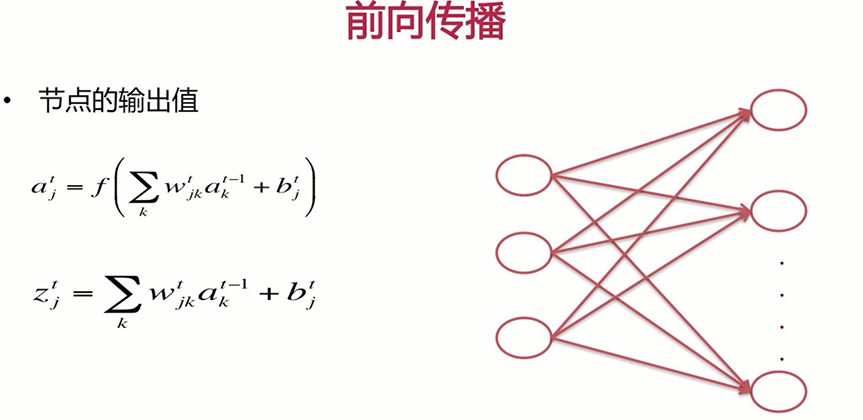
下面我们来了解一下DNN模型的函数表达式,我们只要了解了网络的任何一个节点的输出值也便得到了模型的输出,因为模型的输出实际上就是输出层节点的输出值。
$a_{j}^{t}=f\left(\sum_{k} w_{j k}^{t} a_{k}^{t-1}+b_{j}^{t}\right)$
$z_{j}^{t}=\sum_{k} w_{j k}^{t} a_{k}^{t-1}+b_{j}^{t}$
下面我们来一起看一下公式,下面来解释一下公式,借助于一个简单的网络。t是指的这里的网络中的第t层,t-1呢是t层前面的一层。比如这一层,我们定义为第t层,那么这一层的前一层显然就是t-1层。
如果大家不好理解的话,可以想象一下,当t为0时也便是输入层。当t为1时,便是第一个隐层,当t为大T,便是输出层,这样也许就会好理解一点。a是指的每一个节点的激活值,这里的j表示的是第t个层上我们的这个第j个节点的激活值,这里我们可以把j想象成为1 2…..的节点。如果是1的话,那么便表示第t层上第1个节点的激活值,如果是2的话,并表示第t层上第2个节点的激活值。这里的w是指的第(t-1)层上第k个的节点指向第t层上j这个节点。这里的a同样是激活值,它表示的是第(t-1)层上第k个节点的激活值,b表示第t层上第j个节点的偏移值。如果这里我们求的是第1个节点的激活值的话,那么显然这里也便是第1个节点的偏移值好了。
下面我们以第t层上第1个节点的激活值求值来举例说明一下这个公式。这里呢,如果我们要求第t层上第1个节点的激活值,那么显然我们要依赖于第(t-1)层上,每一个节点的激活值。那么公式应该如下$w_{11}^{t}a_{1}^{t-1}+w_{12}^{t}a_{2}^{t-1}+w_{13}^{t}*a_{3}^{t-1}+b_{1}^t$,最终呢,我们还要加一个$b_{1}^t$偏执,这个偏执得到的加权求和呢。我们再过一下激活函数f,也便得到了我们的激活值。我们把加权求和没有经过激活函数的部分呢定义为$z_{j}^t$。$a_{j}^t$实际上也就是f(z)。
好了,经过我们的讲述呢,我们发现当模型的w与b,也就是所有的参数固定之后呢,我们输入层的特征输入之后,我们第1层的激活值是由我们的输入与w、d参数得到的。第2层呢是由我们第一隐层的激活值呢,与w、b参数达到的,我们这个过程呢是逐步向前去传播。我们把模型根据输入得到输出的过程呢,叫做前向传播。
2.4 反向传播
下面我们来学习一下DNN模型是如何学习我们的参数w与b的。
2.4.1 Our Target
$\frac{\partial L}{\partial w_{j k}^{t}} \quad \frac{\partial L}{\partial b_{j}^{t}}$
我们的目标是什么呢?我们的目标很简单,目标是求得损失函数,对模型中任意两层上两个节点连接的偏导,以及求得损失函数,对任意层上节点的偏置的偏导,如果我们得到了这两个偏导的话,我们发现我们就能将模型中的任意一个参数呢进行梯度下降,这样呢,经过数次迭代,我们最终就能将模型完成收敛,也便学习到了我们需要学的w与b。
2.4.2 What We Have
$\frac{\partial L}{\partial a_{j}^{T}} \quad \frac{\partial L}{\partial z_{j}^{T}}$
我们现在已知的是什么呢?我们现在已经知道了,是损失函数对于输出层节点激活值的偏导,这里的T表示的是输出层,为什么说我们已知道了,我们来详细的写一下公式,假使我们这里的loss函数呢是平方损失函数$(y-a_{j}^{T})^2$。对于每一个样本,我们的损失函数呢是这样的。我们发现以loss函数对于我们这里的输出层的输出激活值,去取偏导的话,很明显的,我们是能够得到答案的,也便是$-2(y-a_{j}^{T})$。同样的这里我们知道了,loss函数对于最后一层节点输出激活值的偏导,也便知道了,我们这里的loss函数对于$z_{j}^T$的偏导,我们来推导一下。用一个链导法则。
$\frac{\partial L}{\partial a_{j}^{T}} \quad \frac{\partial a}{\partial z_{j}^{T}}$
a = f(z)
前一部分呢,是我们已经得到答案的,而后一部分呢,我们又曾经说过a呢,实际上等于我们的f(z), 这里的f是激活函数,所以这一部分呢也很容易求的,所以我们说了我们知道了loss函数,对于最后一层节点激活值的偏导也便知道了loss函数对于z的偏导。
2.4.3反向传播的推导
$z_{j}^{t}=\sum_{k} \mathcal{W}_{j k}^{t} a_{k}^{t-1}+b_{j}^{t}$
$\frac{\partial L}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} \frac{\partial z_{j}^{t}}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} a_{k}^{t-1}$
下面我们来看一下是如何一步一步,通过我们已知的这些东西去进行推导的来看推导,这里我们的目标之一呢是求的loss函数,对于任意节点的偏移,它的偏导,好了这里我们应用一下链导法则,首先呢,我们对loss函数呢,求z值的偏导,既然呢对z值呢,求我们偏移的偏导。
大家应该对这个公式有印象,这个公式是前面我们说的前项传播的公式,所以这里我们看到z值对于b值的偏导呢,实际上是1,因为呢,在z对b偏转的过程中呢,前面这一部分呢相当于是常数。
$\frac{\partial L}{\partial b_{j}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} * \frac{\partial z_{j}^{t}}{\partial b_{j}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} $
$\frac{\partial L}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} \frac{\partial z_{j}^{t}}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} a_{k}^{t-1}$
好了我们再来看一下,loss函数对于任意的网络中的w值,求偏导的整体过程,同样这里我们也采用链导法则,首先呢是loss函数对于z的偏导。z对于w的偏导。
$z_{j}^{t}=\sum_{k} \mathcal{W}_{j k}^{t} a_{k}^{t-1}+b_{j}^{t}$
我们看到z对于任意的w的偏导呢,显然呢,是这里的上一层k节点的激活值$a_{k}^{t-1}$,所以我们看到经过我们的推导呢,我们这里只需要知道loss函数对于任意节点的z值,它的的偏导我们也便得到了最终想要的答案,但是我们这里已知的是我们的loss函数对于我们输出节点的z值,所以说如果我们可以利用倒数第2层节点z值与输出层节点z值之间的关系,逐渐的将loss函数对于输入层节点的z值的偏导,传递的倒数第2层,进而呢由倒数第2层传递到倒数第3层,这样逐一的反向传播,我们便可以得到loss函数对于任意节点z值的偏导,继而我们便得到了loss函数,对于模型参数的偏导,也便完成了我们这里的学习。
2.4.4 反向传播的核心部分
$\frac{\partial L}{\partial z_{j}^{t-1}}=\sum_{k} \frac{\partial L}{\partial z_{k}^{t}} \frac{\partial z_{k}^{t}}{\partial z_{j}^{t-1}}$
$z_{k}^{t}=\sum_{j} w_{k j}^{t} a_{j}^{t-1}+b_{k}^{t}$
$\frac{\partial z_{k}^{t}}{\partial z_{j}^{t-1}}=\frac{\partial z_{k}^{t}}{\partial a_{j}^{t-1}} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}=w_{k j}^{t} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}$
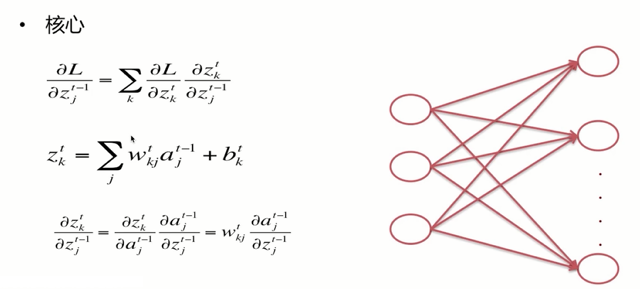
好了下面我们来看推导的最核心的部分,我们说过现在问题的核心呢,变成了如何由损失函数对于输出层节点的。向前传播到倒数第2层,进而传播到倒数第3层,那么这里我们用一个普遍的公式,便是我们知道了第t层的z值的偏导,怎么由第t层z值的偏导呢去推导出第(t-1)层z值的偏导,如果我们知道了这个式子,问题也便解决了,普遍情况下的链导法的是损失函数对$z_k^t$求导,$z_k^t$对$z_j^{t-1}$求导即可。
为什么这里还有一个累加呢?我们借助于简单的网络来说明一下,我们看到这里上一层的任意节点,对下一层的每一个节点都有贡献,都有函数关系,所以我们在$z_k^t$对$z_j^{t-1}$,求偏导时,我们需要每一个节点都算一下偏导,所以这里出现了累加,好了我们将前向传播的式子呢,jk对调一下,我们之前讲前向传播时是求的第t层上第j个节点的a值或者z值。这里呢,我们是求第t层上第k个节点的z值,实际上我们只是把jk对调了一下即可。好了,我们这里呢,损失函数对第t层的z的偏导我们是知道的,因为呢,我们是从最后的T也就是输出层。往前传播的这里只需要求后一部分即可,我们采用链导法的,借助于激活值,我们看到呢后一部分是直接能够得到答案的,因为我们说过a等于f(z),这里的f是激活函数。
同样呢,我们根据这个式子$\frac{\partial z_{k}^{t}}{\partial z_{j}^{t-1}}=\frac{\partial z_{k}^{t}}{\partial a_{j}^{t-1}} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}=w_{k j}^{t} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}$。前一部分呢,也是能够得到答案的,是这里的$w_{kj}^{t}$,既然这样的话,我们的整体流程也便窜了起来,由于我们这里损失函数对于z值偏等的过程中呢,是从后向前求的,所以我们这里的整体流程呢被称为反向传播。
2.4.5方向传播的流程
- 对应输入x,设置合理的输入向量
- 前向传播逐层逐个神经元求解加权和与激活值
- 对于输出层求解输出层损失函数对于z值的偏导
- 反向传播逐层求解损失函数对z值的偏导
- 得到损失函数对于任意节点z值的偏导,也变得到了w与b的梯度
好了,下面我们来看一下整体的反向传播流程是怎么样的,第1步对于从样本中获取的输入呢,我们经过哈希或Embedding等过程呢,设置好合理的输入向量维度,我们根据初始化的模型的参数w与b,逐层的前向传播,这样我们就得到了任意节点的加权和、z值与激活值a值。 然后我们对于输出层求解输出层损失函数对于z值的偏导,这我们是能够得到的,继而反向传播逐层求解损失函数对z值的偏导,这里我们是根据损失函数对$z^t$的偏导与损失函数对于$z^{t-1}$偏导之间的关系反向传播逐层得到的。最终呢,我们得到了损失函数,对于任意节点z值的偏导,也变得到了w与b的梯度,这里我们在推导的时候曾经详细的讲述过。
好了,我们得到了梯度之后呢,便完成了第1轮的迭代,之后呢,我们再逐次将反向传播的过程呢,不停的去进行,直到我们的参数收敛,模型也变训练好了。好了,本小节就到这里,本小节主要讲述了dnn的网络结构以及DNN模型求解的数学原理,下一小节我们将介绍wd模型的网络结构与数学原理。
三、wide and deep的网络结构以及数学原理介绍
开始本小节的课程之前,我们首先来回顾一下上一小节的内容,上一小节我们重点介绍了dnn的网络结构以及数学原理,那么本小节我们将重点介绍wd的网络结构以及数学原理下面开始本小节的内容,下面来看一下本小节的内容会从哪几个方面展开。
1、wd的物理意义,首先会给大家介绍一下wd为什么会优于我们之前单独介绍过的逻辑回归模型,以及上一小节介绍过的深度神经网络。
2、wd的网络结构,会向大家展示一下wd模型是如果构造的。
3、wd的数学原理,我们会一起看一下反向传播算法在wd上是如何进行的。
3.1 wd的物理意义
论文:wide & deep learning for recommender systems
好了下面我们来看一下wd的物理意义。wd出自于谷歌的论文,这篇论文我会在附件中提供给大家,如果大家需要可以读一下这篇论文呢,详述了wd的优点以及wd的网络结构,包括5个在wd上做的一些实验的结果好了下面我们来介绍一下wd为什么会优于我们之前单独介绍过的逻辑回归模型以及深度神经网络模型。
Generalization and memorization 泛化与记忆
首先呢,我们推荐系统当中呢有两个概念,泛化以及记忆,这里的泛化是指的我们推荐的多样性。记忆就比如说某人啊来到我们的推荐系统,一直点击宫斗类型的电视剧,那么这是我们的推荐系统也会一直给他推荐宫斗类型的电视剧,此过程我们称之为记忆,但是呢,这个人也有可能会喜欢历史类型的电视剧的多样性为泛化。我们如何将历史类型的电视剧的特征与该用户的特征在排序时呢,给他学到一个较高的参数呢,如果我们单纯的用逻辑回归的话,我们就需要组合特征,但是组合特征也有一个问题,如果我们的训练数据中没有该用户行为过历史题材电视剧的样本的话,我们的模型也是学不到组合特征对应的参数的,但是呢,深度神经网络DNN是可以的,我们曾经说过,深度神经网络呢可以将我们传入的基础特征进行高维的组合,在隐层当中呢,学出一些高维的特征,但是单独的深度神经网络也有一个问题,如果某用户的行为数据呢并不是十分的充分,那么我们学习的深度神经网络呢,可能会对该用户进行过于的泛化。推荐的结果呢,大多数是他不喜欢的好了,wd的便是能够结合逻辑回归的记忆能力,以及我们深度神经网络的泛化能力,很好的平衡了这两点。
3.2 wd网络结构
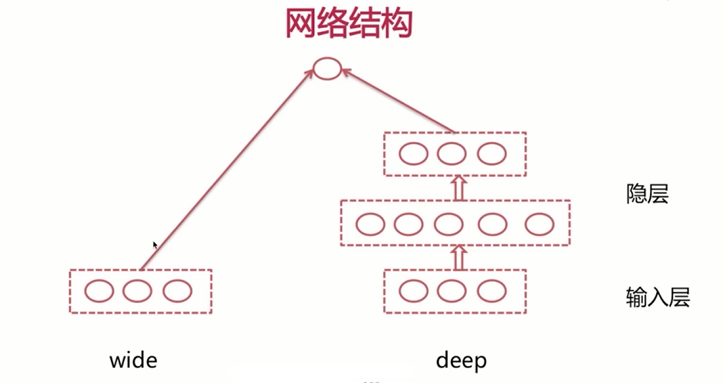
下面我们来一起看一下wd的网络结构,wd的网络结构呢分为两大部分,一部分的是wide部分,这一部分和我们之前介绍过的逻辑回归模型呢,有极大的相似性,比如我们这里输入三个特征,那么它同样呢是将这三个特征呢与对应的参数组合$w1x1+w2x2+w3*x3$,第2部分呢是deep部分,deep部分与我们曾经介绍过的深度神经网络呢,几乎是一样的,这里也分为输入层以及隐藏,当然了,我们这里也是全连接的。
这里唯一与之前所介绍过的有所不同的是,wd模型的输出呢是将(wide侧的参数与特征的加权和)与(deep侧最后一个隐层的输出),做相加在一起经过激活函数,最终得到我们模型的输出。
这样的结构呢,能够保证我们在每一次反向传播的过程中呢,不仅更新地deep侧的参数,同时呢也会更新wide侧的参数,这样也就保证了我们所说的联合训练。通常情况下,我们将离散特征以及离散特征的组合特征放入到wide侧,而我们将连续特征的放入到我们的深度神经网络侧,对于一些字符型的特征,我们通常是先做一下哈希,再做一下Embedding,然后传入到deep侧。
3.3 模型的输出
好了,下面我们来一起看一下模型的输出。模型的输出,包含两部分。
第1部分的是我们的wide侧的输出,这里的x便是我们wide输入的特征,这里的cross便是特征的组合。
第2部分同样的我们这里的deep侧。倒数第2层节点的激活值也就是最后一个隐层的激活值,与我们输出节点与deep侧相连的w的乘积,再加上偏执。
最终2部分的加和呢,要过一下我们的激活函数,这里的激活函数呢是阶跃函数,但是在deep侧的隐层之间的参数学习是我们采用的激活函数是修正线性单元。
3.4 WD model的反向传播
大家一定要注意一下,好了下面我们来看一下反向传播是如何在wd上进行的。
wide参数的学习过程
$\frac{\partial L}{\partial w_{w i d e j}}=\frac{\partial L}{\partial a^{T}} \frac{\partial a^{T}}{\partial z^{T}} \frac{\partial z^{T}}{\partial w_{w i d e j}}=\frac{\partial L}{\partial a^{T}} \sigma^{\prime}\left(z^{T}\right) x_{w i d e j}$
首先呢,我们先来看一下wide参数的学习过程,我们这里采用梯度下降的学习方法,所以呢,我们这里只需要求得,损失函数对于w和任意参数的偏导,也便能够进行参数学习,我们来看一下公式推导,这里采用链导法则。损失函数对w偏导,实际上也就是损失函数对输出层激活值的偏导在乘以激活值,对z值的偏导,在乘z值对参数w的偏大。
损失函数对输出层激活值的偏导,无论我们是采用平方分式函数,还是我们采用对数损失函数,我们曾经都详细的讲过,这一部分的值应该是多少,这里不太赘述。
激活函数的导数计算:我们知道a等于f(z),这里的f就是激活函数,所以呢,这一部分也便是激活函数的导数。我们把$\sigma^{\prime}\left(z^{T}\right) $放进去即可,
最后一部分的,由于我们输出层的输出。实际上我们说过是有两部分的由wide侧以及deep侧,显然呢,我们这里对于wide侧的参数的偏导与deep侧没有关系,也便是我们这里deep侧参数对应的特征。好了,该部分的推导那就讲到这里。
WD model的反向传播
$\frac{\partial L}{\partial z_{j}^{t-1}}=\sum_{k} \frac{\partial L}{\partial z_{k}^{t}} \frac{\partial z_{k}^{t}}{\partial a_{j}^{t-1}} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}=\sum_{k} \frac{\partial L}{\partial z_{k}^{t}} w_{d e e p kj}^{t} \frac{\partial a_{j}^{t-1}}{\partial z_{j}^{t-1}}$
$z_{k}^{t}=\sum_{j} w_{d e e p k j}^{t} a_{j}^{t-1}+b_{k}^{t} \rightarrow t \neq T \quad z_{k}^{t}=\left(\sum_{j} w_{d e e p kj}^{t} a_{j}^{t-1}+b_{k}^{t}\right)+w_{\text {wide}} * X \rightarrow t=T$
下面我们来看一下deep侧参数的学习过程,与我们之前讲述过的dnn网络的反向传播是一样的,我们这里的核心呢都是损失函数,对于输出层z值的偏导,逐渐的前向传播,我们逐渐的得到,损失函数对倒数第2层z值的偏导逐次向前,这里唯一不同的是什么呢?
不同的是我们这里的前向传播的过程呢,如果当我们是最后一层时,我们这里会多出了一些wide侧的特征。
下面来看一下公式推导,这里我们在求上一层损失函数,对z值的偏导时,为什么这里会有一个累加呢?我们在上一小节曾经介绍过,这是因为(t+1)层上任意节点的激活值,都曾经被t层上第j节点贡献过,所以呢,我们需要累加。
好了,我们看到这3部分。
第1部分的,损失函数对于上一层节点的z值的偏导,这里我们是知道的,因为在最开始的时候呢,我们是知道,对输出层z值的偏导逐渐的向前传播,也便知道了t层。
第2部分,中间这一部分呢,根据下面我们两个式子,这两个式子我们分别发现的,虽然带我们的输出层的,我们有wide侧的特征,但是呢,并不影响我们这里求偏导,因为对于我们这里的偏导,wide侧的部分相当于常数,所以我们还是得到了相同的答案。
第3部分,最后一部分呢也是我们刚才说过的,a=f(z)。相当于呢,我们是激活函数的导数,也没有问题。我们得到了损失函数,对于任意层结点的z值的偏导。
$\frac{\partial L}{\partial b_{j}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} * \frac{\partial z_{j}^{t}}{\partial b_{j}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} $
$ \frac{\partial L}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} \frac{\partial z_{j}^{t}}{\partial w_{j k}^{t}}=\frac{\partial L}{\partial z_{j}^{t}} a_{k}^{t-1}$
根据上一小节我们讲过的,此时我们便得到了损失函数,对于deep侧对于每一个偏执以及每一个w的偏导,这样我们便能够进行我们的梯度下降,进行参数学习了。好了,这就是wd模型的反向传播。
3.5server架构
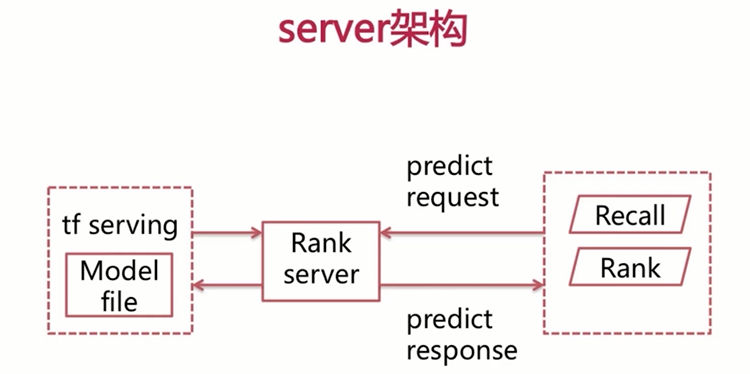
下面我们来看一下,我们得到了最终的模型之后呢,我们是如何与推荐引擎呢进行交互的,这里由于我们采用的是TensorFlow呢,实现我们的wd模型,这里我们必须搭一个TensorFlow serving来提供我们的深度学习的rank服务。
此时呢,推荐引擎呢,需要发动请求到rank server,rank server与TensorFlow serving呢,进行一次交互,将请求呢透传的TensorFlow serving,TensorFlow serving得到的结果呢,返回给我们这里的rank server。rank server再将结果呢透回给我们这里的推荐引擎,来完成每一个item对该user的得分,进而完成排序,我们之前讲述过的浅层模型是rank server可以直接将我们得到的模型文件的load的内存当中,然后利用API呢,去提供打分。
好了,本小节的内容就到这里,本小节重点介绍了wd的网络结构以及数学原理,那么下一小节我们将代码实在wd模型。

