个性化推荐算法实践第03章基于图的个性化推荐召回算法PersonalRank

[TOC]

个性化推荐算法实践第03章基于图推荐的个性化推荐召回算法基于随机游走的Personal Rank

本章节重点介绍一种基于图的个性化推荐召回算法personal rank。从personal rank算法的理论知识与数学原理进行介绍。并结合公开数据集，代码实战personal rank算法的基础版本与矩阵升级版本。

基于图的推荐—基于随机游走的personal rank算法实现

博客第一部分：理论部分主要介绍该算法的背景、物理意义、数学公式推导，以及结合在大数据量实际推荐系统开发工作中为了满足训练速度等方面的要求，对数学公式的矩阵化升级。

博客第二大部分：主要介绍结合第一大部分的数学公式与虚拟log数据为大家编程实战该算法。

1、个性化召回算法Personal Rank背景与物理意义

1、首先介绍基于图的个性化召回算法—personal rank的背景。

（1）用户行为很容易表示为图

图这种数据结构有两个基本的概念—顶点和边。

在实际的个性化推荐系统中，无论是信息流场景、电商场景或者是O2O场景，用户无论是点击、购买、分享、评论等等的行为都是在user和item两个顶点之间搭起了一条连接边，构成了图的基本要素。

实际上这里user与item构成的图是二分图，后面会介绍二分图的概念以及结合具体的例子展示如何将用户行为转换为图。

（2）图推荐在个性化推荐领域效果显著

2、二分图
二分图又称为二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集（A,B），并且图中的每条边（i,j）所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集（i in A, j in B）,则称图G为一个二分图。

（如果有一种无向图，它的定点可以分成两个独立的集合，并且互不相交，且所有的边关联顶点，都从属于这个集合。那么这样的图可以称为二分图。）

则，推荐系统中，user、item恰好满足两种独立的集合，并且用户行为总是从user顶点到item顶点集合，所以由推荐系统中user和item之间构成的图就是二分图。

接下来结合具体实例讲解如何将用户的行为转化为二分图。

假设某推荐系统中有4个用户：A B C D，以及从日志（log）中发现对如下item有过行为：

即：user A 对 item a、b、d有过行为，userB 对 item a、c有过行为，userC对 item b、e有过行为，userD 对 item c、d有过行为。

首先将user、item分成两组不相交的集合，如下：

然后，将所有user 对 item 有过行为的进行连线，就可以得到二分图，如下：

此时问题也就抽象出来了，对于userA 来说，item c 和item e哪个更值得推荐？

这里共有5个item，其中userA 已经对item a、b、d有过行为，这里行为是指信息流产品中的点击或者电商产品中的购买等表示user对item喜欢的这种操作。

那么personal rank恰恰是这么一种算法，它能够结合用户行为构成的二分图，对于固定用户对item集合的重要程度给出排序，也就是说将user A 没有对item c 和item e有过行为，但是personal rank算法可以给出item c 和item e对于user A来说，哪个更值得推荐。

下面从物理意义的角度来分析一下，从二分图上如何分析出来item集合对user的重要程度。

3、物理意义
（1）两个顶点之间连通的路径数

如果要比较两个item顶点对固定user的重要程度，只需分别看一下user到两个item顶点的路径数，路径数越多的顶点越重要。

（2）两个顶点之间连通的路径长度

同样路径数的情况下，总路径长度越短的顶点越重要。

（3）两个顶点之间连通路径经过顶点的出度

这里解释一下出度的概念：出度是指顶点对外连接边的数目。如user A对item a、b、d有过行为，即为有条连接边，则A的出度为3。如果前两项都相同，则两个item对固定user 的重要程度则比较经过顶点所有的出度和，如果出度和越小则越重要。

结合刚才所举的具体二分图的例子，给大家介绍—对于user A来说，item c 和item e哪个更值得推荐？

2、Personal Rank算法example解析

例子分析

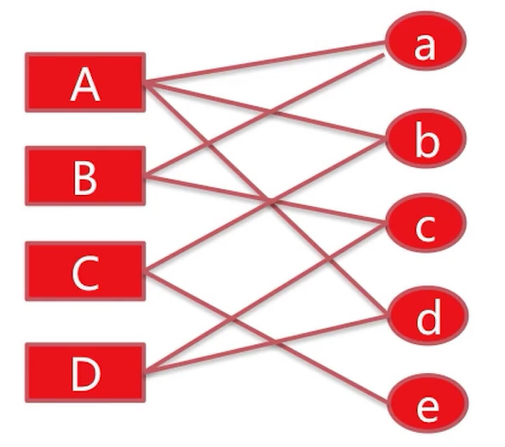
1.分别有几条路径连通？

首先看A-c 之间有几条路径连通：分别是A-a-B-c，A-d-D-c 两条路径连通。

再来看A-e 之间有几条路径连通：A-b-C-e一条路径

从这一角度出发，可以知道 c 比 e 重要。

2.连通路径的长度分别是多少？

首先看A-c 之间有几条路径连通：分别是A-a-B-c，A-d-D-c ，长度都为3

再来看A-e 之间有几条路径连通：A-b-C-e长度为3

3.连通路径的经过顶点出度分别是多少?

首先看A-a-B-c这条路径：A出度是3，a出度是2，B出度是2，c出度是2

再看A-d-D-c这条路径：A出度是3，d出度是2，D出度是2，c出度是2

再看A-b-C-e这条路劲：A出度是3，b出度是2，C出度是2，e出度是1

实例中这里我们物理意义得到的结果。接下来使用程序来完成person Rank算法的时候同样可以得到相同的结论。

虽然 e 的出度和更小，但是由于1中 c 有两条路径，且1的优先级更高，所以还是应该推荐 c。

3、Personal Rank算法公式解析

personal rank是可以通过用户行为划分二分图为固定user得到item重要程度排序的一种算法。

1.算法的文字阐述

随机游走算法PersonalRank实现基于图的推荐对用户A进行个性化推荐，从用户A节点开始在用户-物品二分图random walk，以alpha的概率从A的出边中，等概率选择一条游走过去，到达该顶点后（举例顶点a），由alpha的概率继续从顶点a的出边中，等概率选择一条继续游走到下一个节点，或者（1-alpha）的概率回到顶点A，多次迭代。直到各顶点对于用户A的重要度收敛。

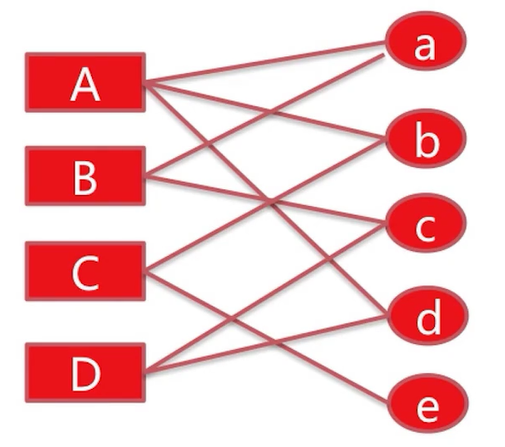
后续我们在实现person rank算法的时候用不同的alpha值来做实验，熟悉是Google的pageRank算法的童鞋们可以发现PageRank与person rank算法有极大的相似性。只不过PageRank算法没有固定的起点。

2.算法的数学公式

$$PR(v)=\left\{\begin{matrix} \alpha * \sum_{v^{\sim} \in i n(v)} \frac{P R\left(v^{\sim}\right)}{\left|o u t\left(v^{\sim}\right)\right|} \ldots\left(v !=v_{A}\right) & \\ (1-\alpha)+\alpha * \sum_{v^{\sim} \in i n(v)} \frac{P R\left(v^{\sim}\right)}{\left|o u t\left(v^{\sim}\right)\right|} \cdots\left(v=v_{A}\right) & \end{matrix}\right.$$

把不同item对user的重要程度描述为PR值。

为了便于理解，同样适用A作为固定起点。user A的PR值初始化为1，其余节点的PR值初始化为0。

这里使用 a 节点和 A 节点阐述公式的上半部分和公式的下半部分：

首先看公式的上部分，根据person rank的算法描述，节点a只可能是节点A与节点B,以alpha概率从他们的出边中等概率的选择了与节点a相互连的这条边。

具体来看，从user A出发有3条边，以3条边中等概率的选择了节点a连接的这条边，以1/3的概率选择连接节点a；user B以1/2的概率选择了连接节点a。

结合阐述看一下公式的上半部分：对于不是A节点的PR值，也就是 a 的PR值，那么首先要找到连接该顶点节点，同时分别计算他们PR值得几分之几贡献到要求节点的PR值。那么A将自己PR值得1/3贡献给了 a ，B将自己PR值得1/2贡献给了 a，分别求和，乘alpha，得到 a 的PR值。

接下来看下半部分：如果要求A节点本身的PR值，首先知道任意节点都会以（1-alpha）的概率回到本身，那么对于一些本来就与A节点相连的节点，比如这里的 a 节点或者 b 节点，它们除了以（1-alpha）的概率直接回到A以外；还可以以alpha的概率从自己的出边中等概率的选择与A相邻的这条边，比如这里的 a 节点，可以以1/2的概率选择回到A节点，所以就构成了下半部分的前后两个部分。

经过分析可以发现，personal rank算法求item对固定user的PR值，需要每次迭代在全图范围内迭代，时间复杂度在工业界实际算法落地的时候是不能接受的，所以要让尽可能多的user并行迭代。结合之前许多其他算法训练的工业界实现，很容易想到矩阵化实现，下面看personal rank算法的矩阵化实现。

3.算法抽象—矩阵式

$r=(1-\alpha) r_{0}+\alpha M^{T} r$

$M_{i j}=\frac{1}{|o u t(i)|} j \in \operatorname{out}(i) e l s e 0$

假设这里共有m个user，n个item。

R矩阵是m+n行，1列矩阵，表示其余顶点对该固定顶点的PR值。当然得到了这个，就得到了固定顶点下，其余所有顶点的重要程度排序，这里只需要排出m个user节点。只看n个item节点对该固定顶点的排序。也就得到了该固定顶点下推荐的item。

r0 是m+n行，1列的矩阵，负责选取某一节点是固定节点，它的数值只有1行唯一，其余行全为0。唯一的行，即为选取了该行对应的顶点为固定顶点。那么得到的就是该固定顶点下，其余节点对该固定节点的重要程度的排序。

M 是 m+n行 * m+n列的矩阵，也就是行包含了所有的节点，列也包含了所有的节点。 它是转移矩阵，数值定义如下：1.第一行第二列的数值距离，如果第一行对应的数值顶点由出边连接到了第二列的顶点，那么该值就为第一行顶点的出度的倒数；如果没有连接边，那么就是0。

我们很容易联想到，第一个式子包含了刚才所说的非矩阵化的personal rank的公式的上下两部分。

$$\left(E-\alpha M^{T}\right) * r=(1-\alpha) r_{0}$$

上述公式是本部分中第一个公式，移项、合并同类项之后得到的。

$$r=\left(E-\alpha M^{T}\right)^{-1}(1-\alpha) r_{0}$$

该公式是上一公式两个同时乘以$\left(E-\alpha M^{T}\right)$转置的之后得到的。

刚才说过，r0是m+n行，1列的矩阵，它能够选取固定的顶点，得到固定顶点的推荐结果。如果将r0变为（m+n）*（m+n）的矩阵，也就得到了所有顶点的推荐结果。

由于得到的推荐结果是考虑顶点之间的PR值的顺序关系，并非一个绝对数值，所以可以将$(1-\alpha) $舍去。所以$\left(E-\alpha M^{T}\right)^{-1}$即为所有顶点的推荐结果。每一列表示该顶点下，其余顶点对于该顶点的PR值。

但是，需要注意的是，每一个user能够行为的item毕竟是少数，所以这里的M矩阵是稀疏矩阵，$\left(E-\alpha M^{T}\right)^{-1}$同样也是稀疏矩阵。