[TOC]

个性化推荐算法实践第09章浅层排序模型gbdt

本章节重点介绍排序模型gbdt。分别介绍梯度提升树以及xgboost的数学原理。并介绍gbdt与LR模型的混合模型网络。最合结合公开数据集，代码实战训练gbdt模型以及gbdt与LR混合模型。

gbdt通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单，并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度，（此处是可以证明的）。

GBDT(Gradient Boosting Tree)背景知识介绍：

由于GBDT(Gradient Boosting Tree)是由Boosting Tree，也就是很多个树模型的组合，首先了解什么是决策树，决策树是如果构建的。

GBDT数学原理与构建方法：

我们需要这个GBDT模型是如何将很多个树模型组合在一起，并且发挥了比一颗树更大威力的。

XGBoost数学原理与构建方法:

XGBoost是陈天奇提出的GBDT一种改进与落地方法，由于其高性能以及优良的表现，在工业界广泛使用。

从头了解Gradient Boosting算法：https://blog.csdn.net/qq_36510261/article/details/78875278

GBDT(Gradient Boosting Decision Tree)入门（一）：https://blog.csdn.net/qq_38150441/article/details/80343626

一、GBDT(Gradient Boosting Tree)背景知识介绍

介绍什么是决策树，并且向大家展示分类与回归树是如何构建的（决策树是如果构建的）。

1、什么是决策树

树的数据结构大家都应该了解，树有根节点，左右子树，叶子节点等等组成。

什么是决策树呢？在决策树中我们可以这样认为，叶子节点对应的是模型的输出，其余节点每一个节点对应特征。而决策树呢，就是样本在该节点对应的特征由于取值的不同划分到左右两颗子树里面。同时呢，在左右两颗子树里面再利用对应的节点，将数据划分，最终呢会划分到某一叶子节点，便完成了模型的输出。

大体的流程就是这个样子，如下图。我们以上一小节的曾经举过的实例来简单讲解一下。

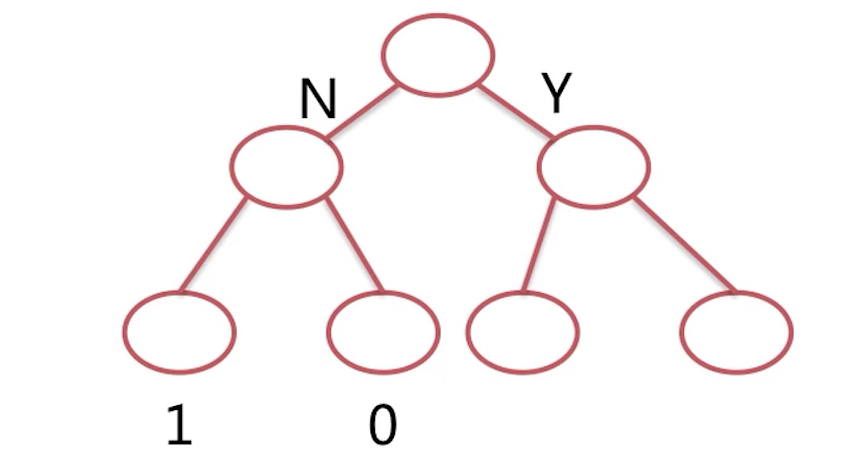
1566459385812

比如说这里根节点对应的特征呢，是给没给女朋友买礼物，如果给了的话，那么该样本数据呢就会落到右子树当中，如果没有没有给啊，那么显然呢，要么会落到左子树当中。那么再依据新的节点，这个节点对应的特征可能是说陪没陪女朋友是没有吃饭，如果是陪了的话那么继续往下，没有陪的话那么继续往下到左子树，这样呢，我们一直到叶的节点，叶子节点呢表示模型的输出，由于该实力呢是2分类问题，所以拿叶子结点的输出呢，便是0或1表示呢女朋友是否开心，当然了，树模型也可以是回归树，比如呢，我们在预测某人的身高这个问题上，那么最终的叶子节点可能会输出180、175cm, 相信经过上面的介绍，大家已经对决策处有了一个初步的了解。

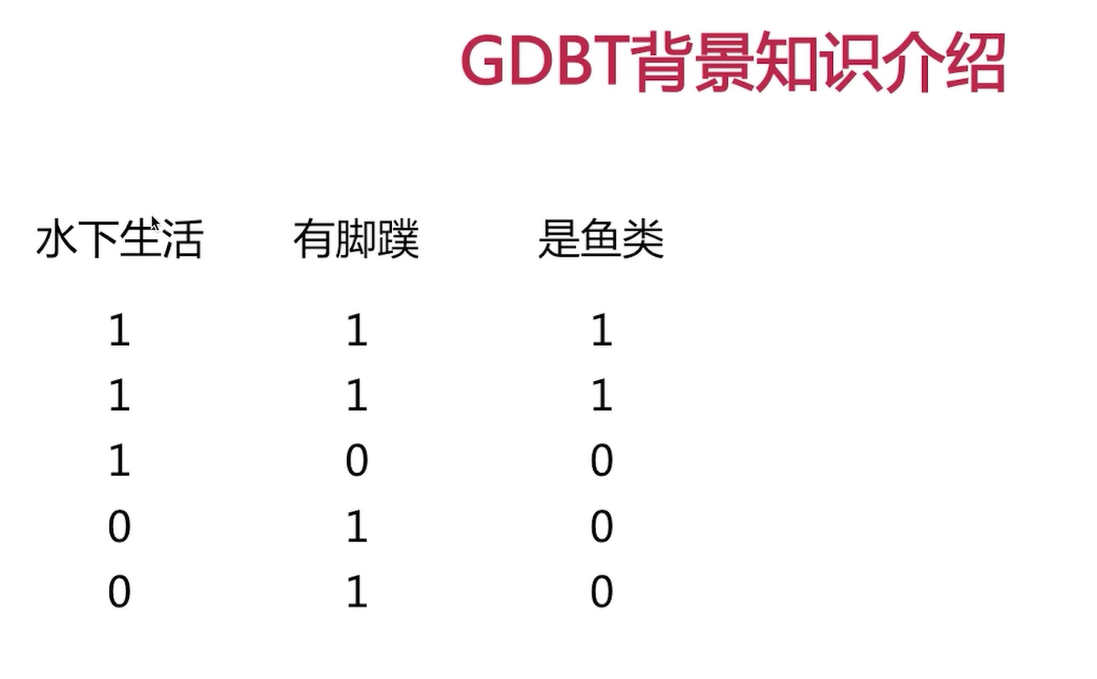
1566471769876

下面我们以一组具体的样本来给大家详述一下决策树的构建过程。我们这里有一组训练样本，这个样本呢，有5条数据，然后呢有两个特征，是否在水下生活以及是否有脚蹼，当然了它的label呢是是否鱼类，是一个二分类问题，我们看到这里5组数据呢特征的取值都是0、1，一表示带水下生活，一表示有脚趾，好了，那么我们构建出的决策树应该是什么样呢？是这样的，根节点对应的特征是是否在水下生活？如果不是的话，我们发现没在水下生活的那么很明显对应的label，全都不是鱼类，那么这里也就直接到了叶子节点，也就不是。好了，如果是在水下生活的话，我们看到在水下生活，但是呢，有是鱼类也有不是鱼类的。所以我们这里需要再借助一个特征，也就是有没有脚蹼。我们发现在水下生活，并且有脚蹼的话，图片很明显都是鱼类。如果在水下生活，并且没有脚蹼的话便不是鱼类。这就是我们基于这五条训练数据得到的模型，那么这个模型是如何工作的呢？在新的样本输入进来的时候，比如说不在水下生活也没有脚蹼，那么我们的模型是如何给出预测的呢？首先呢，不在水下生活，直接就会预测不是鱼类，这便是决策书的工作流程，我们已经了解了什么是决策处，但是哪一个特征应该是优先特征帮我们把样本到左右两颗子树，以及整体的决策树构建的流程，我们还不是很清晰，下面来一起了解一下。

2、决策树构造原理

1、CART生成
2、回归树：平方误差最小化原则（CART生成算法构造回归树）
3、分类树：基尼指数（CART生成算法构造分类树）

决策树生成

生成算法	划分标准
ID3	信息增益
C4.5	信息增益率
CART	基尼指数

2.1、CART生成

CART算法原理及实现：

https://blog.csdn.net/hewei0241/article/details/8280490
https://blog.csdn.net/gzj_1101/article/details/78355234

这里介绍的决策树生成树的算法是CART算法，分类回归树算法：CART(Classification And Regression Tree)算法。CART中的“C”表示分类，CART中的“R”呢表示回归，当然了，我们决策树生成的算法呢，还有很多，比如说ID3、C45等等等等，这里为了与后面的知识介绍，GBDT其实相连，所以这里我们选用了CART生成算法进行介绍。

CART生成算法，既可以构造回归树。当然了构造回归树我们采用的原则是平方误差最小化。CART生成算法，也可以去构建分类树。构造分类树时，我们采用基尼指数作为选取最优划分特征的依据。

下面我们分别来看一下回归数与分类数的构造。

2.2、回归树：平方误差最小化原则（CART生成算法构造回归树）

2.2.1 回归树的函数表示

首先呢，我们来一起看一下回归树的函数表示：

$f(x)=\sum_{m=1}^{M} c_{m} I\left(x \in R_{m}\right)$

这里的M表示一共有M个叶子节点，$R_{m}$表示m叶子节点对应的区域，如果我们输入的样本属于这个区域的话，这里公式中的I便为1。如果不属于，公式中的I便为0。也就是说我们的样本是属于这个区域的话，这里公式中的I便为1。如果不属于，公式中的I便为0。
也就是说如果我们的样本是m区域，那么对应的输出为$c_{m}$。

${\sum_{x_{i} \in \mathcal{R}_{m}}\left(y_{i}-f\left(x_{i}\right)\right)^{2}}$ ${c_{m}=\operatorname{ave}\left(y_{i} | x_{i} \in R_{m}\right)}$

$c_{m}$的定义需要满足在m区域的所有样本对应的模型的输出，与自己label差的平方和是最小的。显然$c_{m}$应该等于在m区域所有样本的label的平均值。

下面介绍回归树如何选取最优划分特征。也就是说哪一个特征应该放到根节点，哪一个特征应该放在第二层的节点。

2.2.2 最优划分特征

j表示的是特征，s表示的是特征取值的一个临界分隔值。

如果这个特征取值$x^j$比这个临界分隔值s小的话，我们便划分到第一部分

如果这个特征取值$x^j$比这个临界分隔值s大的话，我们便划分到第二部分

对应第一部分和第二部分，有一个常数值，就是常数c，这个c是怎么定义的呢？c是属于区域所有样本的平均值。

倾向性得分。

区域的lable做差。

可以以18做划分

也可以

最优化的划分。

2.2.3 树的构建流程

遍历所有的特征，特征的最佳划分对应的得分，选取最小的得分的特征

遍历所有的特征，特征的最佳划分对应的得分，选取最小的得分的特征为最优特征，会将其放在根节点。

将数据依据此选取的特征划分分成两部分

基于此特征我们将数据分为两部分，也就是树的左右子树。

继续在左右两部分遍历变量找到划分特征直到满足停止条件

在左右子树里，我们再继续进行上面的操作，继续寻找最优划分特征。当然呢，在左右子树里，根节点特征被拿掉了，我们继续这一个流程，直到满足停止条件。在回归树当中呢，停止条件有两个。一是子树中只剩下一个特征。二是达到了我们之前设定的树的深度。

对应分类树来说呢，同样，如果说子树中label只剩下一种分类或者说特征只剩下一个，也是要进行停止的。

分类树与回归树的构建流程是一致的。但是分类树的最佳划分特征选取的是基尼指数。

2.3、分类树：基尼指数（CART生成算法构造分类树）

基尼指数公式

${\operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}}$ ${D_{1}=\{(x, y) \in D | A(x) \geq a\}, D_{2}=D-D_{1}}$ ${\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)}$

对于某样本D的基尼系数是由上述公式求解的。公式中的$C_k$表示样本中的第k个分类它的样本数。分母表示总的样本数。如果这个样本只有一个分类，我们发现这个样本的基尼系数为0。这也是我们希望看到的。

如果我们将样本中的某特征以a为临界值进行划分，我们便得到了$D_1$,$D_2$两个部分。对于特征A以a为邻近值划分下的基尼指数了，也便是我们的第一的基尼系数加上第二的基尼系数，当然了这里都是带权的，这个权重呢，也便是我们划分的第一的样本除以总的样本的数目第二。第2个样本除以总的样本的数目。

下面我们以一个具体的例子来解释一下这个公式，这个实例呢，是我们之前介绍什么是二叉树的时候曾经用。

好了下面我们来看一下水下生活这个特征，它的基尼指数是多少呢？这里显然呢，水下生活这个特征只能以01为划分。这样呢，我们划分水下生活这个特征成的第一呢是占了3/5，然后这里面呢有2/3的呢，是1是鱼类这个分类，也就是1减去2/3的平方，再减去哪1/3的平方也就得到了4/9【1-（2/3）^2 - (1/3)^2 = 4/9】。我们看到零它占了2/5，但是呢，零对应的所有的内部呢都是一样的，也就是说呢，1减去1的平方也就成了0【1-(2/2)^2=0】，所以呢，对于水下生活这一个特征，它的基尼指数呢是12/45，≈0.26667。

我们再来。看一下是否有脚趾这样一个特征，它的基尼指数，我们看到呢，它将样本划分成了两部分，一部分呢占据4/5，然后呢，这里面呢它应该是呢，1-1/2的平方再减去1/2的平方也就得到了2/4【1-（1/2）^2 - (1/2)^2 = 1/2】，也就是1/2，然后呢，另一部分呢是1/5，然后呢乘以呢，是什么呢？1-1的平方也就是0【1-(1/1)^2】，最终呢他得到的是4/10。

显然呢水下生活它的基尼指数更低一点，它是零点二几，是否有脚趾的基尼指数是0.4。所以说呢，我们的根节点呢，应该用是否在水下生活。本小节的内容到这里就全部结束了，本小节重点讲述了GDP的背景知识决策数，讲述的决策处是什么以及决策处如何构建。

防止回归树过拟合：回归树剪枝（预剪枝和后剪枝），控制树的生长（如控制树深），在树每次生长的时候对一些特征进行采样，甚至可以加一些限制条件比如说在叶子节点上最少要多少个样本。叶子节点少于10个样本是不可以的。必须要在阈值样本数量才可以进行学习。

二、梯度提升树的数学原理与构建流程

集成学习Ensemble Learning ：Bagging 和 Boosting相关的博文

Bagging和Boosting 概念及区别：https://www.cnblogs.com/liuwu265/p/4690486.html

Bagging与随机森林算法原理小结：https://www.cnblogs.com/pinard/p/6156009.html

Bagging（Bootstrap aggregating）、随机森林（random forests）、AdaBoost ：https://blog.csdn.net/xlinsist/article/details/51475345

bagging和boosting 总结，较全：https://blog.csdn.net/u014114990/article/details/50948079

集成学习Ensemble Learning与树模型、Bagging 和 Boosting、模型融合：https://blog.csdn.net/sinat_26917383/article/details/54667077

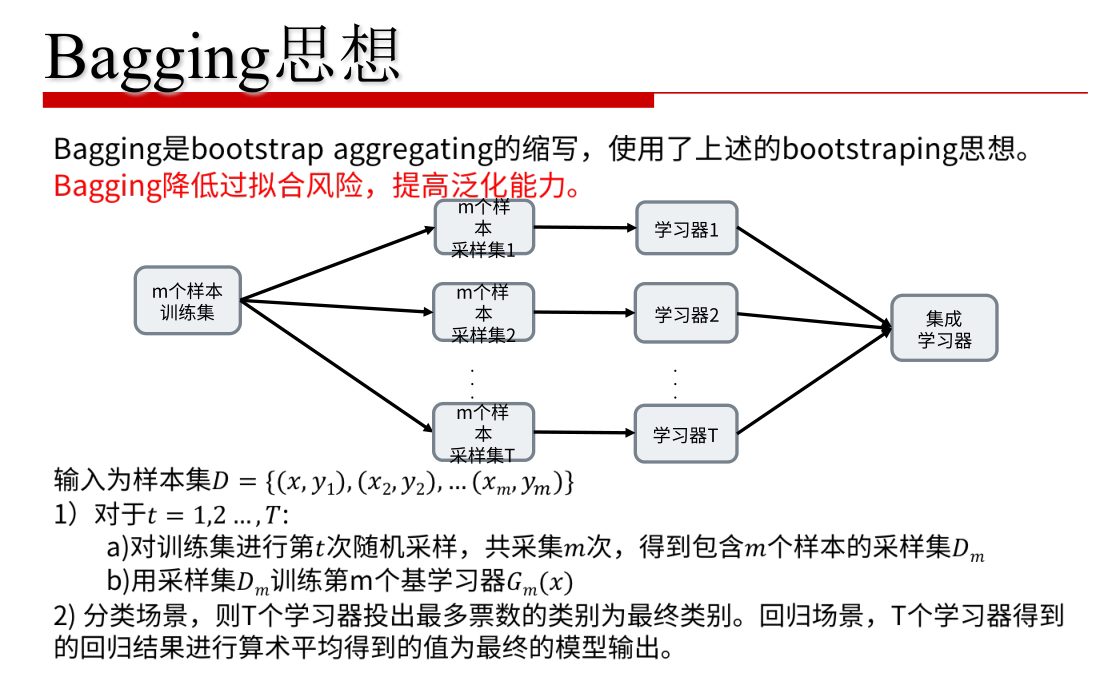
1568567063198

1568567108682

Boosting与Bagging主要的不同是：Boosting的base分类器是按顺序训练的（in sequence），训练每个base分类器时所使用的训练集是加权重的，而训练集中的每个样本的权重系数取决于前一个base分类器的性能。如果前一个base分类器错误分类地样本点，那么这个样本点在下一个base分类器训练时会有一个更大的权重。一旦训练完所有的base分类器，我们组合所有的分类器给出最终的预测结果。

本次的个性化推荐算法实战课程主要从boosting来进行梯度提示树的学习。

2.1 boosting

什么是boosting

大家好，欢迎来到本次的个性化推荐算法实战课程，开始本小节的课程之前，我们首先来回顾一下上一小节的内容，上一个小节我们重点讲述了决策处的构建过程，那么本小节我们将重点介绍梯度提升数的构建过程，下面开始本小节的内容，我们首先来看一下什么是提升方法，其实我反而有这么一种基本的思想，对于一些复杂的任务，无论是回归问题还是分类问题，如果许多专家得出的结论会比其中某一专家得出来的结论更加靠谱，这就是我们俗语说的三个臭皮匠顶一个诸葛亮的道理，那么问题来了，我们在实际的任务中呢学习一个非常非常良好的模型是比较费力的，而学习很多弱的模型呢是比较简单的，如果我们能将这学习到的许多热的模型组合起来，也就完成了我们提升方法的思想，也就通过群体决策来战胜了一个强大的模型，那么无论是对于分类问题还是回归问题，实际上呢提升方法呢，就是从弱学习模型开始出发，反复的学习，得到一系列的弱分类器或回归器将它们组合的，里面构成了强大的模型，大多数提升方法都是通过改变训练数据的权重或者说改变训练数据的值，来完成对于弱模型的学习，这样对于提升方法来说呢，有两个问题需要考虑。

1、第一个问题是每一个弱模型的学习过程中呢，我们怎么改变训练样本的值？或者说是训练样本权重的分布？2、第二个问题呢是如何将这些弱模型的组合成一个强模型？

如何改变训练数据的权重

我们来分别看一下第一个问题如何改变训练数据的权重和值。我们以分类问题来举例，对于刚开始学习到的弱分类器，我们在下一轮学习做分类器的过程中呢，我们会减弱那些被上一轮分类器正确分类的样本，而去增加那些上一轮弱分类器分类错误的样本的权重，这样一来便可以对那些没有被正确分类的样本重点照顾，只有这样才能再将多个弱分类器组合的过程中呢，有希望战胜一个强大的分类器，

如何组合多个基础model
第2个问题如何组合多个基础的模型，我们在训练得到了多个弱模型之后呢，不同的提升方法的处理是有所不同的，比如像业界比较著名的ada提升方法的便采用了加权表决的方法，具体的在分类问题呢，它会加大分类误差率较小的弱分类器的权重，使其在表决中呢起到更大的作用，那么对于梯度提升术呢，这里显然呢，它采用的是等权的加和也就是每一棵树呢，它起到的作用都是相同的，对于回归问题呢也是如此，下面我们来看一下提升树的具体的数学原理。

2.2 Boosting Tree

提升树模型函数

${f_{M}(x)=\sum_{m=1}^{M} T\left(x ; \boldsymbol{\theta}_{m}\right)}$

首先呢，我们看一下提升数的函数表示，这里呢，我来解释一下公式，这是每一棵树它的函数表示，那么这里的提升树呢，由M棵树来构成，每一棵树呢，大家都可以把它想象成上一节我们讲过的决策树，$\theta$是这一棵树的参数，好了，我们看到呢，每一棵树呢都是等权相加的，那么这样的一个提升树模型，我们是怎么样来进行学习的呢？

${f_{m}(x)=f_{m-1}(x)+T\left(x ; \theta_{m}\right)}$

这里呢，我们采用前项分布的算法，这是一种启发式的学习方法，他能够保证了在每一轮的学习当中呢，只学习一棵树的参数，这样有什么好处呢？我们以一个简单的例子来说明一下，如果提升树一共有十棵树，那么我们在学习第一棵树的时候也就是$f_1$,那么嘛，他显然就等于$t_1$，但是$f_2$他等于$f_1$加上$t_2$，这里呢，由于$f_1$已经变成了已知了，那么此时我们只需要学习$t_2$，它保证了我们每一轮的迭代都是可学习的。

${\boldsymbol{\theta}_{m}=\arg \min _{\theta_{m}} \sum_{i}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+T\left(x_{i} ; \boldsymbol{\theta}_{m}\right)\right)}$

这样我们如何去学习$t_2$呢？只需要按照我们的损失函数。在损失函数上的我们只需要最小化这个公式就可以，$y_{i}$是样本对应的label,$f_{m-1}\left(x_{i}\right)$这是我们上一轮已经学习到的函数，这是$T\left(x ; \theta_{m}\right)$我们这一轮待学习的函数

这样启发式的方法保证了我们的可学习性，如果我们不采用启发式的方法，大家看一下这里我们的LOSS函数${f_{M}(x)=\sum_{m=1}^{M} T\left(x ; \boldsymbol{\theta}_{m}\right)}$应该是$f_{M}$，$f_{M}$的话这里相当于每一轮不是有一棵树的参数需要学习，而是有M颗树需要学习。那是根本没法学习的。

2.3 迭代损失函数

$L(y, f(x))=(y-f(x))^{2}$
$L\left(y, f_{m}(x)\right)=\left[y-f_{m-1}(x)-T\left(x ; \theta_{m}\right)\right]^{2}$

下面我们来一起看一下迭代过程中的损失函数，如果我们的损失函数呢，采用我们之前经常讲的平方损失函数的话，那么第m颗树的学习就变成了下面这个公式，我来解释一下，这里的y是label，这里的$f_{m-1}(x)$是上一轮迭代迭代完成之后，我们的函数变成的样子，也就是说我们第m颗树的学习，只需要去拟合上一轮我们迭代完成$f_{m-1}(x)$之后这个模型对于最终样本的偏差度我们把这个称为残差。

举一个例子比如说我们要预测某人身高，那么在上一轮迭代的过程中呢，我们已经预测出了一米75，而这个label是1米80，那下一次我们第m个树的学习呢，只需要去拟合这5cm的差距，也就是说样本的label变成了5。而不是一米80。上面介绍了一个回归的例子，实际上对于我们的应用场景点击率过来也可以看成是一个回归问题。因为我们这里可以预估出他的点击倾向性，我们设定一个阈值，比如说点击倾向性大于等于了我们这个阈值，那么我们就认为是会点击，如果小于了我们设定的阈值我们就认为是不会点击。所以呢，同样可以让它去拟合这个label与这个点击倾向性之间的差，也就是残差。

2.4 提示树的算法流程

初始化$f_0(x)=0$

对m=1,2…M计算残差$r_m$,拟合$r_m$,得到$T_m$

更新$f_m = f_{m-1} + T_m$

下面我们来看一下提示树的算法流程。第一步初始化$f_0(x)=0$，对于第一颗树第二颗树直到第M个颗树，我们依次计算残差，并且用这颗树去拟合这个残差，并且得到相应这颗树。比如说，我们第1轮的时候$f_0(x)=0$，所以说呢，残差还是label本身我们便得到了$T_1$，那么对于第2个树呢，我们首先计算残差，也就是label的减去$f_1$的值，我们去拟合这一个值得到$T_2$，以此类推，我们今天能够得到每一棵树，直到得到了M。那么我们每一轮训练完一棵树之后呢我们便更新这个公式。也就是说呢，$f_2$等于$f_1$加上$T_2$，这个时候呢，我们得到了f2，对于我们训练$T_3$的时候呢，首先呢，计算残差也就是label减去$f_2$，那么$T_3$的也便去拟合这个label得到了$T_3$，以此类推呢，我们这里f3也就得到了，最终呢，我们得到$f_M$，也便完成了整个提升树的训练，下面我们以一组具体的训练样本为例来详述一下提升树的构建流程。

1566823913657

首先来看一下训练样本，这里的训练样本呢，只有一个特征x，只有一个输出的y，x的分布呢是1~10，label是一些浮点数，我们首先来回想一下决策处的构建过程，我们首先要找到最佳划分的特征，由于这里只有一个特征的，我们只需要找到x的最佳划分，也便是我们第1棵树的根节点特征，这样的训练数据就会被分为左右两颗子树，我们只需要分别计算左子树的label的平均值和右子树label的平均值。也便得到了$T_1$。

我们首先来看一下，怎么来寻找最佳特征的划分？这里我们首先呢以1为划分点，我们看到了小于等于1的是一区域，大于1的是二区域，这里呢，将两个区域呢，分别变成了一区域[1]，二区域[2-10]，c1呢就是一区域所对应的label的平均值，也就是5.56，同样的c2是什么呢？C2是二区域[2-10]对应label的平均值，这里的是7.5，我们会得到一个倾向性的得分，这个倾向性的得分呢便是，一区域里所有的数据label与c1的差的平方和我们看到的只有一个数据，差的平方和是0。

1566823913657

1566824388831

然后呢2区里所有的数据label与我们c2的差的平方的和也就得到了15.72。这样的，我们遍历了所有的分割点我们看到的123一直到9，我们都是可以分割的，这样呢，我们得到了对优的分割的应该是6，也就是说小于等于6的一组，大于6的是另外一组，那么可是我们得到了$T_1$，$T_1$是什么呢？在特征小于等于6的时候呢，它的值呢是6.24，也就是说，所有label的平均值，在特征大于6的时候呢，它的输出呢是8.91，也是这个区域所有label的平均值，这里呢，我们的呢，f1就等于f0+T1，由于我们初始化f0=0。所以呢，我们得到了f1，这个时候呢，我们只需要计算一下残差，也就是说，此时呢变成了label减去f1，我们看到呢上面讲过的，label是5.56，减去6.24等于-0.68。, 以此类推这里我们得到的残差。

我们继续再找到队友划分，再完成这一棵树的学习也就达到了72 t2呢，这里它是以单为最佳划分的，它的输出分别是哪？负的0.52以及呢0.22，这时呢，我们便得到了f2，f2=什么呢？等于f1+t2，f1呢是这里的t1，所以呢，我们的f2呢也就变成了一个单段的分段函数，分别是特征小于等于3，此时呢输出了便是6.24与负的0.52的和以及特征大于3到特征小于等于6，此时的输出是6.24与0.22的和以及第3部分也面试，特征的大于6，此时输出了也是八年级。9一与0.22的和，那么我们继续整个流程，直到我们训练完大m棵树，页面结束了，我们提升速度的学习好了，了解了提升术的学习方法，我们来一起了解一下梯度提升术的学习方法，当我们的损失函数是平方损失或者指数损失的时候，每一步的优化呢是不那么困难的，但对于一般的损失函数而言呢，每一步的优化并不是特别容易，所以呢，梯度提升数呢，只是将我们的盘差变为了什么呢？变为了损失函数的负7度，在当前模型的曲子，那么我们下一棵树呢，只要去拟合这个值便得到了t小m好了，本小节的内容到这里就全部结束了，本小姐。人员予以构建流程，那么下一小节我们将给大家介绍插队故事的数学原理与构建流程。

2.5 梯度提示树

残差的数值改变

$r_{m}=-\left[\frac{\partial L\left(y, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)-f_{m-1}(x)}$

三、xgboost数学原理介绍

开始本小节的课堂之前，我们首先来回顾一下，上一小节的内容，上一小节我们重点讲述了梯度提升数的数学原理与构建过程，那么本小节我们将带大家一起学习一下XGBOST的数学原理与构建流程，XGBOST的数学原理，陈天琪博士曾经公开过一份PPT，我也会在附录里提供给大家方便大家的学习。

下面开始本小节的内容，我们首先来看一下XGBOST的函数表示。

3.1 XGBoost模型函数

$f_{M}(x)=\sum_{m=1}^{M} T\left(x ; \boldsymbol{\theta}_{m}\right)$
$f_{m}(x)=f_{m-1}(x)+T\left(x ; \theta_{m}\right)$
$\arg \min _{\theta_{m}} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+T\left(x_{i} ; \theta_{m}\right)\right)+\Omega\left(T_{m}\right)$

同样呢，这里呢，也是有多棵树构成，我们知道多棵树构成的这种学习方法呢，也是使用我们前面讲述过的前项分布，同样呢，既然是前项分布算法，我们就需要优化出这个目标函数，这样呢，我们在每一次学习的过程中呢，就能够学习到一棵树，将这一棵树的参数学习好之后呢，我们再累加起来逐次迭代，这样呢，就能够学习到最终的M棵树。

这里与我们前面讲述的不同的是呢，对于每一棵树都有一个正则化项，也就是说当我们学习第小m棵树的时候呢，会设定一个小m这棵树的正则化，它表示小m这棵树，它的参数的复杂程度，具体的公式后面我们会详细介绍。

如果大家还记得上一节课我们在讲提升树时，对于小m这棵树，我们只需要你和label与$f_{m-1}$的残差即可构建出小m这个树，如果是梯度提升树的话，我们也只需要去拟合损失函数的负梯度，在当前的函数值，当前呢，指的是$f_{m-1}$。

3.2 优化目标的泰勒展开

目标函数：$\arg \min _{\theta_{m}} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+T\left(x_{i} ; \theta_{m}\right)\right)+\Omega\left(T_{m}\right)$

泰勒展开公式：$f(x+\Delta x) \approx f(x)+f^{\prime}(x) \Delta x+1 / 2 f^{\prime \prime}(x) \Delta x^{2}$

根据泰勒展开公式优化的目标函数：
$\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\Omega\left(T_{m}\right)$

$g_{i}=\frac{\partial L\left(y_{i}, f_{m-1}\right)}{\partial f_{m-1}}, h_{i}=\frac{\partial^{2} L\left(y_{i}, f_{m-1}\right)}{\partial f_{m-1}}$

但是呢XGBoost采用了另一种思路，我们来看一下，首先呢，我们先介绍一下泰勒公式，相信呢，大家对这个公式呢，都不是很陌生，泰勒公式的二阶段展开是这样的$f(x+\Delta x) \approx f(x)+f^{\prime}(x) \Delta x+1 / 2 f^{\prime \prime}(x) \Delta x^{2}$。我们的优化目标，可以把这一部分($y_{i}, f_{m-1}\left(x_{i}\right)$)看成x，加号后面的部分$T\left(x_{i} ; \theta_{m}\right)$看成$\Delta x$，那么我们便可以按照泰勒公式进行展开。展开之后呢，我们的目标函数得到的是什么呢？

$\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\Omega\left(T_{m}\right)$

第1部分显然呢是loss，在$f_{m-1}$, 这个函数下的loss，对于我们的优化目标来说呢，我们此时构建小m这棵树，那么log在$f_{m-1}$这个地方，它就变成了常数，常数呢对于我们的优化目标是不需要的，我们需要的是损失函数的导数在当前模型的值，以及损失函数的二阶导在当前模型的字，分别对应上面的函数的导数与函数的二阶导数，我们前面说过$\Delta x$呢，看成了这里的$T_{m}$。所以呢，我们便得到了优化目标。

3.3 定义模型复杂度

$f(x)=\sum_{j=1}^{Q} c_{j} I\left(x \in R_{j}\right)$
$\Omega\left(T_{m}\right)=\partial Q+0.5 \beta \sum_{j=1}^{Q} c_{j}^{2}$

下面我们来看一下正则化项部分是如何定义模型参数的复杂度。XGBoost里，所有的树呢，都是回归树，我们在讲决策树的时候曾经讲过回归树的模型呢，可以这样$f(x)=\sum_{j=1}^{Q} c_{j} I\left(x \in R_{j}\right)$进行表示，这里呢一共有Q个区域，每一个区域的输出值呢是c，我们讲过c呢，实际上是在该区域所有的样本对应的label的平均值。

好了，我们把复杂度$\Omega\left(T_{m}\right)=\partial Q+0.5 \beta \sum_{j=1}^{Q} c_{j}^{2}$定义为所有的叶子结点的数目，以及呢，每一个叶子结点对应的输出的平方，当然了这里有两个正则化的系数。

这种定义方式的让我们联想到了曾经讲述过的逻辑回归的正则化，非常像我们曾经讲过的，l1正则化与l2正则化，这里的0.5呢与我们前面的泰勒展开呢，相对应我们来看一下，泰勒展开里呢，也有一个0.5，所以呢，我们后面呢，把0.5呢从我们的智能化系数当中的提取出来，我们看到这里的优化目标呢，是从每一个训练样本的角度去进行考虑的，为了接下来我们在构建树的过程中呢，好展开我们的思路，这里呢，我们将优化目标进行一下转化。看一下是如何转化的。

3.4 目标转化

${\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\Omega\left(T_{m}\right)}$ ${\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\partial Q+0.5 \beta \sum_{j=1}^{Q} c_{j}^{2}}$ ${\min _{\theta_{m}} \sum_{j=1}^{Q}\left[\left(\sum_{i \in R_{j}} g_{i}\right) c_{j}+0.5\left(\sum_{i \in R_{j}} h_{i}+\beta\right) c_{j}^{2}\right]+\alpha Q}$

1、本来优化目标函数：

${\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\Omega\left(T_{m}\right)}$

这是我们本来的优化目标，它是按照样本的维度N 。我们首先呢把正则化项$\Omega\left(T_{m}\right)$写入进来。

2、目标函数：

${\min _{\theta_{m}} \sum_{i=1}^{N}\left[g_{i} T_{m}+0.5 * h_{i} T_{m}^{2}\right]+\partial Q+0.5 \beta \sum_{j=1}^{Q} c_{j}^{2}}$

3、被转化后的目标函数：${\min _{\theta_{m}} \sum_{j=1}^{Q}\left[\left(\sum_{i \in R_{j}} g_{i}\right) c_{j}+0.5\left(\sum_{i \in R_{j}} h_{i}+\beta\right) c_{j}^{2}\right]+\alpha Q}$。

我来解释一下公式，之前的我们说过$T_m$每一个样本的输出呢，实际上也就是对应的区域$c_j$的输出，也就是这里的$c_j$。

每一个样本都会对应到每一个叶子节点，这里假使我们小m这棵树呢，一共有10个叶子结点，那么很明显，我们所有样本的输出都会归结到这10个叶子结点。

这里需要重点考虑一下损失函数的一阶导与二阶导。

只需要将样本是属于这一个叶子节点的一阶导，放到这一个区域$c_j$的前面，比如说c1在一个区域，我们的一阶导呢是说我这个样本如果它属于c1这个区域。那么，我的这个样本呢，它对应的一阶导便是其中的一个系数，我们将这个系数累加起来也就是这一部分。

同样的如果呢，如果这个样本是属于c1这个区域，我们将它的二阶导也累加起来当做它的区域。这里呢，合并了一下同类项，把我们的智能化系数呢也合并进来了。就变成了下面这个式子。

就是说遍历所有的样本，变成了遍历所有的叶子节点，相信大家也应该能够理解了。

可能这里大家对本次函数的一阶导二阶导的概念不是很清晰，我们以一个简单的例子来说一下，我们就以这个损失函数呢，是我们长距离的平方根式函数。那么它对于这个FM减1的一阶导应该是什么呢？应该就等于呢，也很简单，就等于那二位的WiFi，减去哪，FM点c，那前面还有一个符号，二跌倒是什么呢？二跌倒就是在这个的基础上呢，再对FM减1求一次等，很明显的就得到2，下面我们来一起看一下目标函数的最优解，我们这里定义了一下大j与大h，那么目标函数呢，就变成了如下这个样子，显然呢，这是一种ax的平方加bx的行驶。我们知道，但是这种形势下呢，如果a是大于0的话，他便是开口向上的抛物线，他的最小值的取代x=负的分母是二倍的a分子呢，是b的情况下，那么好了，这里同样是当我们的c呢取代，负两倍的这一部分，然后呢分子呢是大j的情况下，显然也就是当c等于这一部分的时候，整体的，我们的优化目标函数呢，将会取得最小值，最小值也变是这个式子，我们来一起看一下我们是如何使用目标函数的最小值，去选取我们的最优划分特征的。这是我们获得的目标函数的最小值。我们在cc布什里是依据如下这个公式来选取我们的最优化分特征的，这里呢，我简单解释一下，比如呢，我们这里以年龄这个特征为例，依据年龄呢以18岁痕迹，大于18岁的呢，挖到了左边，小于等于18岁的呢，挖掉了右边，那么这时呢，我们只需要将整体的目标函数的最小值分别减去左半部分目标函数的最小值，再减去右半部分目标函数的最小值，这里的鱿鱼多了一次化身的，会使燕子节点的数目增加1，所以呢，还需要减去一下郑德华的系数，我们遍历完所有的划分，比如说18岁为划分25岁为划分等等等等，得到的最大的收益便是该特征下最佳划分，那么我们遍历所有的特征。每个课堂对应的收益的最大值，也便是我们首先要放到根节点上的特征，进而呢不停的去构建我们的树，直到满足我们前面讲述过的停滞条件，我们来看一下caccabc，第1步呢，也是初始化f0，进而呢对于第1棵树以及之后的每一棵树呢，都应用我们刚才讲述过的，选择最优划分特征的方法呢，去构造树，对于构造完成的数量，我们将它并不是100%的放入到模型当中的，这里会有一个不长，这个不长的，在程序中的默认值是0.3，主要是为了防止过拟合，好了，这就是xz boss的模型的总体流程，那么本小节的内容到这里就全部结束了，本小节重点介绍了xx模型。与总体流程，那么下一小节我们将给大家介绍gbdt模型与逻辑回归模型的混合模型。

四、gbdt模型与逻辑回归LR模型的混合模型

个性化推荐算法实战课程开始本小节的课程之前，我们首先来回顾一下上一小节的内容，三位小姐我们重点介绍了差距boss的模型，数学原理与构建流程，那么本小节，我们将重点介绍GB dt与lr的混合模型，下面开始本小节的课程，下面来看一下背景知识，本小节所讲述的GDP与lr模型的混合模型，是出自于当年Facebook所发表的一篇论文，他的题目呢？我贴在你这里，他的paper呢我也会付给大家，如果大家感兴趣的话可以读一下关于GDP与l2模型混合模型的构建思路，主要的原因是什么呢？是因为我们知道我们在构建逻辑，回归模型是需要繁琐的特征处理，如果大家还记得我们在讲逻辑回归模型的构建过程中的时候，我们。与特征的处理，要对特征进行分类，将特征呢分为连续特征与离散特征，对于连续特征，我们首先要统计它的分布，然后呢，按照区间段进行特征的离散化对于离散特征，我们需要统计它的值域，然后呢，进行我们的特征离散化，当然呢，这些特征处理完之后呢，我们还要进行组合特征的筛选，这个过程呢将非常的繁琐，而且呢组合特征需要手动来执行，那么我们并不能完全的发挥出组合特征的威力，所以呢，逻辑回归模型的训练呢是非常非常的繁复，而恰巧我们的树模型呢在连续特征处理时，是不需要进行这么繁琐的处理，我们只需要把连续特征输给数，然后呢数倍基于我们前面讲述的一系列的最优划分特征。去将最优的划分点给选取出来，也就相当于呢，进行了一系列的规则转化，最终呢，将所有的输出的落到某一叶子节点上，那么对于一旦特征呢，我们也是需要刚开始呢，将它进行零一编码，也就是弯号的编码编程，我们可以识别的零一特征，然后呢，在进行我们刚才说过的这一系列的操作，最终呢也是将某一样本的收入呢落到具体的某个燕子节点上，而我们的GDP模型呢，有很多棵树，每一棵树呢都是一样特征，转化到了某一个业主节点上进行输出，那么我们看到实际上在不同的数的输出当中的我们相当于把特征的变换成了一种新的特征，这一新的特征呢是经过我们数内部的结构去进行不断的筛选转化的。高危特征呢，我们再把它放到逻辑回归模型里去训练，得到我们的参数，这时呢，两者模型便能有效的结合，下面我们来一起看一下模型的结构，我们首先来看一下GB dt模型的第1棵树的结构，这里的树的深度呢是2，我们看到呢，他有四个燕子结顶，大家来看一下第2棵树的结构，同样呢，它的深度呢也是2也有4个叶子结点，但是呢，要么对于在数一当中的输出呢是落到了第2个一的节点，要么对于数2的输出呢是落到了第4个电子结点，此时呢，我们便可以进行高为特征的编码，第1个数的编码也就是0 100, 第2个书的编码也就是0001，大家这里对电的节点有概念吗？可以联想一下我们前面讲。绝色素的模型的输出输出的函数是你的小c，如果大家不进的话，我简单的写一下。这里的c也便是我们这里所说的燕子姐姐，由于这里的树的深度是2了，所以一共有4个区域，如果我们样本最终呢属于哪个区域，也就是我们这里我说的，你也没别的，所以呢，我们便将它对应的，落到第几个月的节点，这一位的编码程序，其余的编码成0，这样呢，我们便得到了高为特征，由于这里的我们一共有两棵树，所以呢，这里它都能围住，是吧，如果我们GB dt模型里数的数占多一点数的深度呢，也算深一点，那么懂得特征的维度呢，也会变得更高，这里我们得到了高危的转化特征之后呢，便可以用来训练我们的逻辑回归模型，这里需要训练的是w1到w8这8个参数好了，这边是我们的GDP。LI混合模型的网络结构，但是大家这里一定要注意一下这里的训练呢，不是联合训练，是我们的样本，首先训练得到数之后再将样本呢，通过数呢进行编码，得到我们的高为特征，用高为特征呢再去训练我们的lr模型，最终呢，我们在线上预测的时候呢，也是需要我们首先呢将数模型保存，然后呢，将lr模型的参数呢也保存样本过来之后呢，先通过数模型进行特征的转换，然后呢，再将转化完成的特征呢，与我们训练得到的参数呢，去得到我们最终的结果，下面我们来看一下gpdt模型与l2模型，混合模型的优缺点分析，首先来看一下优点，优点呢便是利用数模型的做特征转化，这样呢既可以节省了我们。为逻辑回归模型去手动构造特征的繁琐工程量，同样呢，又利用了数模型能够将特征的较好的处理，而不需要大量的手动工作量的特点，可谓是强强联合，但是呢，它同样也有缺点，它的缺点呢是两个模型的是分别训练的，并不是联合训练，并不是联合训练的，就没有统一的目标函数，没有统一的目标函数呢，理论的可解释性就不强，但是无论如何呢，这种尝试呢也是有创新性的，在我实际的工作经验中呢，发现l2与GDP的混合模型的效果是要比GB dt单独的模型以及l2单独的模型效果要更加好的，本小节的内容到这里就全部结束了，本小节重点讲述了GB dt与lr混合模型的相关制度。那么下一小节我们将带大家一起代码实战GDP模型的训练。