[TOC]

个性化推荐算法实践第04章基于深度学习的个性化召回算法item2vec

本章节重点介绍一种基于深度学习的个性化召回算法item2vec。从item2vec的背景与物理意义以及算法的主流程进行介绍。并对该算法依赖的模型word2vec数学原理进行浅析。最后结合公开数据集代码实战item2vec算法。

本章节重点介绍基于深度学习的个性化召回算法item2vec。分为两部分：第一部分，item2vec背景和物理意义，论文依据，算法流程，以及item2vec的依据的模型word2vec的数学原理等等理论部分解析。第二部分，根据示例数据，item2vec的算法流程，编程实战，训练模型得到item对应的向量完成推荐并分析推荐结果。

一、基于深度学习的个性化召回算法item2vec

1、个性化召回算法item2vec背景与物理意义

个性化召回算法item2vec背景

1. Item2item的推荐方式效果显著：

很多场景下item2item的推荐方式要优于user2item；

item2item的推荐方式：在获取item相似度矩阵之后，根据用户的最近的行为，根据行为过的item找到相似的item，完成推荐，如itemCF。

user2item：根据用户的基本属性和历史行为等基于一定的模型，算出最可能喜欢的item列表写在KV存储中；当用户访问系统的时候，将这些item列表推荐给用户，像userCF、LFM、personal rank算法等都是这种方式。

1. NN model（神经网络）模型的特征抽象能力

神经网络的特征抽象能力是要比浅层的模型特征抽象能力更强，主要有两方面原因：

（1）输入层与隐含层，隐层与输入层之间，所有的网络都是全连接的网络；

（2）激活函数的去线性化；

基于上述，基于神经网络的item2item的个性化召回算法item2vec也就在这个大背景下产生了。

3、依据的算法论文：Item2Vec: Neural Item Embedding for Collaborative Filtering

核心内容1：论文首先介绍了item2vec落地场景是类似于相关推荐的场景。也就是说用户点击了某item a APP,那么推荐一款类似的APP给用户。

核心内容2：介绍了item2vec所选的model，也就是word2vec算法原理，文中采用了负采样的训练方法进行介绍，因为我们知道word2vec还有一种也就所说的哈夫曼树的方式进行训练。那么我们后面也用负采样的方式进行介绍word2vec的算法原理。

核心内容3：论文抽象了算法的整体流程。

核心内容4：论文将给出了与之前流行的item2item算法进行结果对比。

个性化召回算法item2vec物理意义

在介绍item2item之前，先介绍一下原型word2vec。

1. word2vec

根据所提供的语料，语料可以想象成一段一段的文字，将语料中的词embedding成词向量，embedding成词向量之间的距离远近可以表示成词与词之间的远近。（word2vec原理中详细介绍怎么样做到可以表征词与词距离的远近）

1. item2item

（1）将用户行为序列转换成item组成的句子。

解释：在系统中，无论是用户的评分系统，还是信息流场景下用户的浏览行为，或者是电商场景下用户的购买行为。在某一天内，用户会进行一系列的行为，那么将这一系列的行为抽象出来。每一个用户组成的item与item之间的这种序列的连接关系就变成了之前所说的文字组成的一段一段的句子，那么这里的每一个word相当于这里的item。

（2）模仿word2vec训练word embedding 过程，将item embedding。

word embedding的过程只需要提供语料，也就是一段一段的文字，那么训练得到的word embedding可以表征词语义的远近，那么同样希望表征item之间内涵的远近。

所以，可以将第一步构成的item语料放到word2vec中，也能够完成item embedding。embedding完成的向量同样可以表示item之间的隐语义的远近，也就是说，可以表示item之间的相似性。

以上就是item2vec的物理意义。

个性化召回算法item2vec缺陷

（1）用户的行为序列时序性缺失：

在介绍物理意义的时候，说过将用户的行为转化成由item组成的句子，这里句子之间词与词之间的顺序与按照用户行为顺序进行排列和不按照用户行为顺序进行排列的结果是几乎一致的。

也就是用户的行为顺序性，模型是丢失的。

（2）用户行为序列中的item强度是无区分性的：

这里比如说，在信息流场景中，观看短视频的50%或者80%或者100%，在用item组成的句子当中，同样都是出现一次的，而不是说观看100%就会出现2次。

再如，在电商场景中，可能你购买一件商品，或者说你加了购物车，都会出现一次；而不会说，你购买了就会出现两次。加了购物车，在句子当中出现一次。在item cf算法中，item 相似度矩阵计算 ，当时引入了用户行为item的总数，用户行为item的时间这两个特征，来分别将公式进行升级。所以在item2vec算法中，是没有这个消息的。所以是item2vec的缺陷之一。

2、item2vec算法应用的主流程

（1）从log中抽取用户行为序列

按照每个用户“天”级别，行为过的item，构成一个完整的句子，这里的行为根据不同的推荐系统所指的不同。比如：在信息流场景下，用户点击就可以认为是行为；那么在评分系统中，我们可能需要评分大于几分；在电商系统中，可能希望用户购买，得到用户行为序列所构成的item句子。

（2）将用户序列当做语料训练word2vec得到item embedding

在训练过程中，word2vec代码不需要书写，但是有很多参数是需要我们具体设定的。

（3）得到item sim关系用于推荐

根据第二个步骤中得到每一个item所embedding的向量，可以计算每一个item最相似的top k个，然后将相似度矩阵离线写入到KV当中，当用户访问我们的推荐系统的时候，用户点击了哪些item，推出这些item所最相似的top k个给用户，就完成了推荐。

eg：

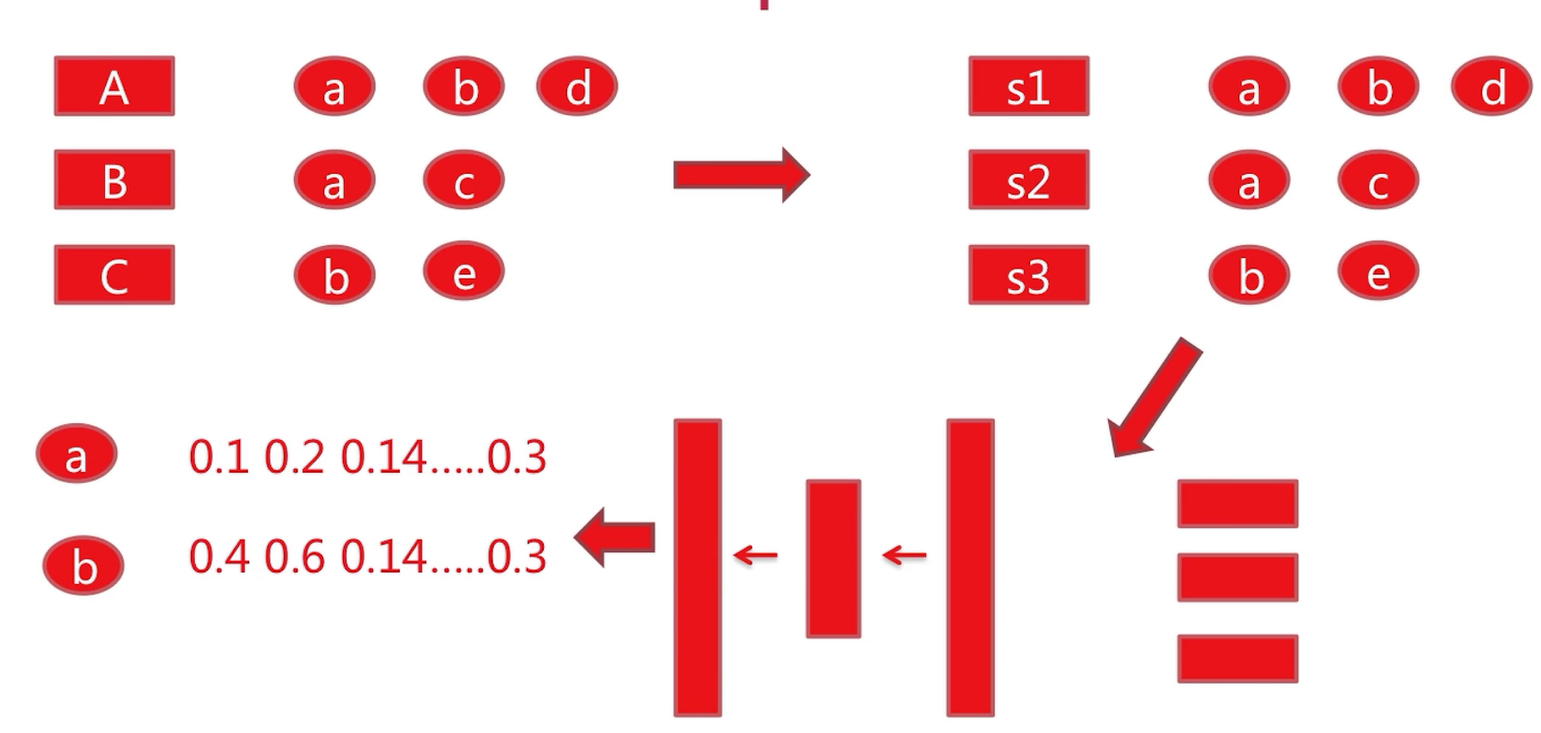
1、首先第一步：这是我们从推荐系统log中获得的，也就是说User A行为过item a、item b、item d，User B行为过item a、item c，User C行为过item b、item e。

2、继而我们需要将这些转化成句子。句子1就是a、b、d。句子2就是a、c。句子3就是b、e。这里我们已经没有了user之间的关系，只留下item组成的句子。

3、将句子放入到放入word2vec模型，这里就是一个输入（word2vec模型是一个三层的神经网络：输入层、隐含层、输出层，具体每一层的作用，公式原理后面详细介绍。）

经过word2vec模型的训练，会得到每一个item对应的embedding层向量。这里只写了item a [0.1,0.2,0.14……..0.3] ,item b [0.4,0.6,0.14……..0.3]。item c，item d,item e也是可以得到的。

4、得到item向量之后，就得到item的sim关系。基于item sim的关系，我们便完成了用户的推荐。

3、item2vec依赖模型word2vec介绍（连续词袋模型和跳字模型(skip-gram)）

item2vec依赖模型word2vec的数学原理详细介绍

word2vec model

是围绕负采样的训练方法进行介绍，因为我们知道word2vec还有一种也就所说的哈夫曼树的方式进行训练（这里就不做介绍了）。

word2vec有两种形式：连续词袋模型和跳字模型(skip-gram)

1. CBOW（continuous bag of words）连续词袋模型
2. skip gram()跳字模型

二、item2vec依赖模型word2vec之CBOW数学原理介绍

1、CBOW网络结构

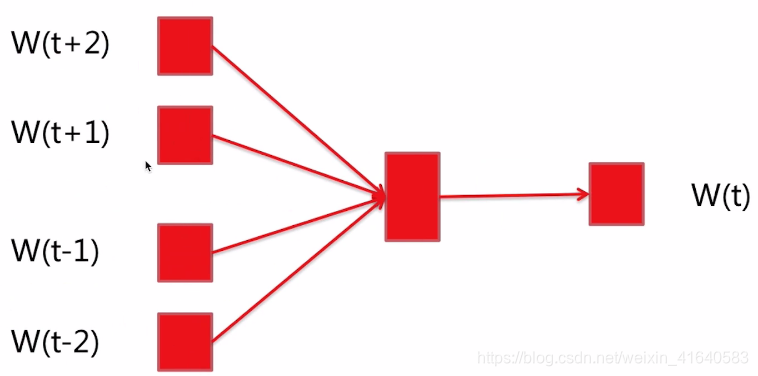
网络分为三层：输入层、投影层、输出层。

输入层：上下文；比如说这里有五个词W(t+2)、W(t+1)、W(t)、W(t-1)、W(t-2)。这里我们需要输入的训练数据是W(t)的上下文，即是W(t+2)、W(t+1)、W(t-1)、W(t-2)。

投影层：将上下文的词输入的向量加起来；因为给每个词都初始化了一个向量。比如说我们需要让它的长度是16。那么刚开始的时候，这些词W(t+2)、W(t+1)、W(t-1)、W(t-2)，再包括了W(t)都有一个初始化的向量。把这些向量加到了投影层。

输出层：当前词；

投影层与输出层之间是全连接，如果输出的这个词是这里的W(t)的话，希望最大化的就是这个概率。而除了W(t)，词典（词典指训练语料包含的所有的词）中所有的其他的词，其余词的概率我们都希望最小那个概率。

这就引申出一个问题，如果其余词都是负样本的话，负样本太多，训练太慢。

所以，采用负采样（后面介绍）的方法。这里我们先不要关心负采样的具体是怎么做的，后面我们会详细的介绍

也就是说，有了正样本W(t)与它的上下文，负样本是通过负采样得到的，我们希望最小化负样本所对应的模型的输出。这里实际上，最后一层的输出不仅仅是只有W(t)，实际上是有字典中每一个词。因为每一个词都有一个与输出层之间的全连接，这也是模型需要训练的参数之一。

然后，模型需要得到的是每一个词，我们初始化的那个向量，让它训练，根据我们传入的训练样本，训练完成的向量，就是最后模型输出。我们就是依赖每一个词对应的向量，完成item相似度矩阵之间的运算。

与传统的监督模型有所不同，传统的模型在训练完成之后，需要将它保存，然后对外提供服务，当我们传入真实样本的时候，希望得到一个输出值；而这里不是。下面我们来看下一中形式。

2、CBOW的数学公式

1. 问题抽象

$$g(w)=\prod_{u \in w \cup N E G(w)} p(u | \operatorname{Context}(w))$$

上式是想最大化的条件概率函数。

下面我来解释一下这个公式：

$\text { Context }(w)$：某一词W(t)的上下文的词，已知上下文，想预测中间词。

可能有的同学对于这个训练样本还不是很了解，下面我举一个最简单的例子，有一句话是我是中国人，那么经过分词之后呢，变成了（我 是 中国 人）这么四个字也就是w1,w2,w3,w4，如果我们选窗口是1的话，在这里第1组的训练样本变成了（我 是 中国 人），其中这个”是”就是公式这里的w，它的上下文呢，w(t+1)呢是’中国’，w（t-1）是”我”这个词。

我们知道了”中国”，”我”这个词。如果u是W的话（这个u是公式中W”是”的话），则是需要最大化条件概率；如果是W的负样本（NEG(w)）（除了”是”，以外的其他词），我们想要把这个概率最小化，最小化这个条件概率$p(u | \text { Context }(w))$，也就是最大化$1-p(u | \text { Context }(w))$条件概率。那么无论是u是w,或者u是我们选择的负采样的负样本都能统一起来了，实际上这个式子由两部分组成。

这里的条件概率是指：

$$p(u | \text { Context }(w))=\sigma\left(X_{w}^{T} \theta^{u}\right)^{L^{w}(u)}\left(1-\sigma\left(X_{w}^{T} \theta^{u}\right)\right)^{\left(1-L^{w}(u)\right)}$$

这个式子由两部分组成：

（1）当u=w时，也就是说label $L^{w}(u)$=1，起作用的是前一部分，因为后面的指数变为零次幂（$1-L^{w}(u)$=0），零次幂的话，后面部分就等于1了。起作用的是前一部分，我们是想最大化的正样本的概率。解释一下这里的$X_{w}^{T}$和$\theta^{u}$：

$X_{w}^{T}$：CBOW的时候，投影层是将w对应的上下文的词向量加和。也就是我们这里举例子的”我”和”中国”对应的向量加和，便是这里的$X_{w}^{T}$。

$\theta^{u}$：隐含层（投影层）和输出层对应的词为u的时候，它们之间的全连接。

所以，想通过模型训练，让这两个参数$X_{w}^{T}$和$\theta^{u}$相乘得到的结果为1。（按照我们的距离就是16维的横竖向量相乘应该是一个常数，这里我们希望通过训练，让他最终相乘得到的数字是1）

（2）负采样部分，也就是后面那一部分，我们这里负采样选取的负样本，希望这一部分是0。也就是希望这一部分$1-\sigma\left(X_{w}^{T} \theta^{u}\right)$为1，也就是最大化$1-\sigma\left(X_{w}^{T} \theta^{u}\right)$这一部分。

1. 损失函数

$\operatorname{Loss}=\log (g(w))$

这里采用对数损失函数，之前LFM采用的是平方损失函数。

公式带入：

$$\text {Loss}=\sum\left(L^{w}(u) * \log \left(\sigma\left(x_{w}^{T} \theta^{u}\right)\right)+\left(1-L^{w}(u)\right) * \log \left(1-\sigma\left(x_{w}^{T} \theta^{u}\right)\right)\right)$$

取对数之后，简单讲解一下，之前的累乘，由于我们取对数，就变成了累加。而之前里面是两部分相乘，，由于我们取对数，就变成了两部分相加。而且对数里面的幂次，可以直接变成了这里的系数。

对$X_{w}^{T}$和$\theta^{u}$求偏导，求完偏导之后，使用梯度上升法不断迭代这里我们这里需要的参数$X_{w}^{T}$和$\theta^{u}$，继而便能够去迭代每一个词对应的词向量。

1. 梯度：

$\frac{\partial L o s s}{\partial \theta^{u}}=\left(L^{w}(u)-\delta\left(x_{w}^{T} \theta^{u}\right)\right) x_{w}$ $\theta^{u}=\theta^{u}+\alpha * \frac{\partial L o s s}{\partial \theta^{u}}$

$\frac{\partial L o s s}{\partial x_{w}}=\left(L^{w}(u)-\delta\left(x_{w}^{T} \theta^{u}\right)\right) \theta^{u}$ $v(w_{context}) = v(w_{context}) + \sum_{u \in w \cup NEG(w)}\alpha *\frac{\partial L o s s}{\partial x_{w}}$

梯度公式1：

首先对$\theta^{u}$求偏导得到了上述的结果。我们先不在此处讲解推导过程。推导过程和排序部分的逻辑回归的部分完全一样。（推导过程也并不是很复杂，只需要记住链式求导法以及加上激活函数。sigmod函数的导数是等于他的本身乘以（1-他的本身），即是s(x)*(1-s(x))）。这两个小技巧比较容易得到。

公式中，$L^{w}(u)$是label，值是1或者0，如果当这里的词是中心词的时候就是1，如果这里的词是负采样中选取的负样本，那么就是0。$\delta\left(x_{w}^{T} \theta^{u}\right)$这个是模型的输出,实际上是投影层对应的向量$x_{w}^{T}$，并且乘以$\theta^{u}$向量得到的一个值，我们在用激活函数激活一下，也得到了一个零一之间的值。这里的$x_{w}$便是投影层上下文向量的加和。

由于我们之前看到的损失函数里$x_{w}$与$\theta^{u}$是对偶的，所以loss函数对$x_{w}$的偏导也便是与上面对偶的形式，只不过括号外面是乘以$\theta^{u}$。

梯度公式2：

既然分别都得到偏导之后呢，我们如果去更新呢。对于$\theta^{u}$我们根据学习率去对于$\theta^{u}$更新就可以了。但是对于$x_{w}$更新，我们看到由于这里损失函数对$x_{w}$求偏导呢，是与这里的$\theta^{u}$有关系的。这个u我们知道它有可能是中心词，也有可能是负采样所选出来的负样本，所以他是一系列的，我们将这一系列的词，或者说是正负样本对。学习完之后我们得到一个总的梯度。得到这个总的梯度之后呢，是$x_{w}^{T}$的梯度，也就是$x_{w}^{T}$可以去更新它自己。这里$x_{w}^{T}$是所有上下文词向量的加和。这里也采用了上下文的每一个词都共享这个梯度，来更新自己的向量。

这里就是$x_{w}^{T}$对于正负样本对他的梯度的加和。然后我们将上下文中的每一词对应的词向量都以这个梯度去更新。

3、训练的主流程

1. 选取中心词w以及负采样出NEG(w)

   根据训练的语料，选取中心词w与上下文的词构成的正样本以及负采样选取出的负样本。

2. 分别获得损失函数对于$X_w$和的$\theta^u$梯度

$X_w$：隐含层(投影层)的向量，是上下层向量的一个累加和；

$\theta^u$：正负样本的每一个词都有一个$\theta^u$；

1. 更新$\theta^u$以及中心词对应的上下文context(w)中的每一个词的词向量。

这里更新的时候需要注意：

以一个实例来说明：

中心词所对应的负样本，假使我们选了5个，加上中心词与上下文组成的正样本，这里一共有6个样本。在$X_w$的梯度的过程当中，实际上是6个梯度的加和，构成了它自己的梯度。在每一词所需要更新的$\theta^u$以及$X_w$的1/6的时候，首先先更新$X_w$的1/6。因为$X_w$是依赖于$\theta^u$的。如果这一次我们将$\theta^u$更新呢，再更新$X_w$的话，就错了。

故需要先更新$X_w$，在更新$\theta^u$。

三、item2vec依赖模型word2vec之skip gram数学原理介绍

1、skip gram网络结构

我们首先来看一下它的网络结构，这里同样有三层构成(输入层、投影层、输出层)。

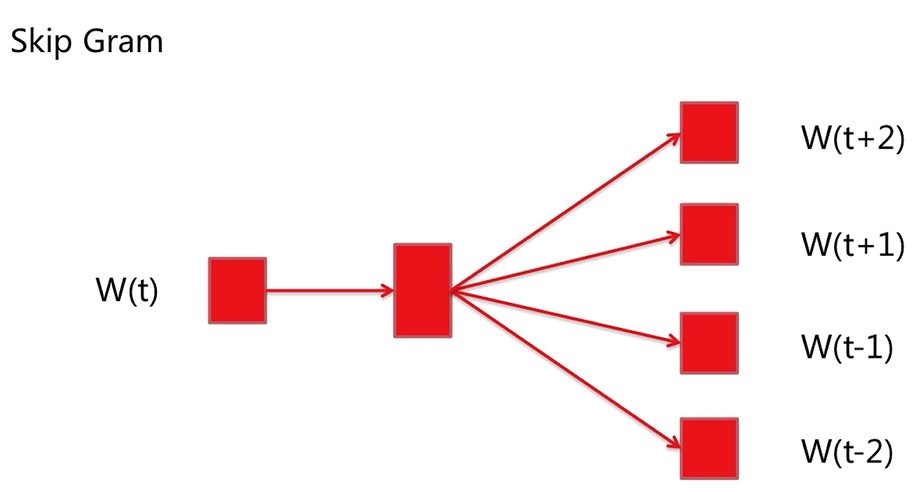
与CBOW网络结构不同的是，这里的投影层与输入层完成是一样的，也就是说，投影层是W(t)的输入向量。

这里的核心目标是说，当W(t)已知的情况下，去预测它的周围词，我们将这个条件概率最大化就是我们的目标。所以，这里也是有两组参数需要更新的：

（1）W(t)与词典中的每一个词所对应的这种全连接网络，这个参数需要更新；

（2）W(t)本身对应的初始化的向量。比如说我们想要把每个词映射成16维，这个向量也是需要更新的，

这里与之前有两点不同：

（1）这里每一次更新，只能更新W(t)一个词语对应的向量；而CBOW模型一次可以更新4个（4：针对上图）。也就是对应的这个上下文，如果我们上下文的窗口选的更长一点的话，可能会更新的更多一次。

（2）在对W(t)的每一个词进行上下文训练的时候，都需要对输出的词进行一次负采样，来构成训练的负样本。

2、skip gram的数学公式

1. 问题抽象

$$G=\prod_{u \in \text { Contert }(w)} \prod_{z \in {u} \cup NEG(u)} p(z | w)$$

skip gram是已知中间词，去最大化它相邻词的概率。

举个栗子：”我 是 中国”为例子，这个w就是”是”这个词。这里的z就是”我”或者”中国”他们对应的正样本，以及通过负采样选取的负样本，最大化正样本的输出概率，并且最小化负样本的输出概率，也就是最大化(1-负样本）的输出概率。

与CBOW的不同：CBOW的时候，是选取一次负采样；而这里对于中间词的上下文的每一个词，也就是”我”或者”中国”,每一次都需要进行一个负采样。

下面看一下条件概率：

$$p(z | w)=\left(\delta\left(v(w)^{T} \theta^{z}\right)\right)^{L^{u}(z)} *\left(1-\delta\left(v(w)^{T} \theta^{z}\right)\right)^{1-L^{u}(z)}$$

这个条件概率与之前的CBOW大体形式一样，也就是说当label $L^{w}(u)$=1的时候，我们还是希望最大化这个条件概率。当label $L^{w}(u)$=0的时候（看后半部分），我们需要最大化$(1-\delta\left(v(w)^{T} \theta^{z}\right))$,即最大化1减去模型输出。

这个条件概率与之前的CBOW，不同之处：

（1）隐含层（投影层）输出的是中间词对应的词向量；而CBOW是输出的所有中间词上下文词向量对应的和；

（2）这里的$\theta^{z}$：上下文的词，或者是上下文的词选出来的负样本的词与输出层之间的全连接；目标是中间词$v(w)^{T}$对应的向量以及$\theta^{z}$进行参数学习。进而得到中间词词向量的最佳表示。

1. 损失函数 $$\text {Loss}=\sum_{u \in \text {Context}(w)} \sum_{z \in {u} \cup N E G(u)} L^{u}(z) * \log \left(\delta\left(v(w)^{T} \theta^{z}\right)\right)+\left(1-L^{u}(z)\right) * \log \left(1-\delta\left(v(w)^{T} \theta^{z}\right)\right)$$

采用log损失函数。将上述的式子log一下，两个连乘，变成了两个连加（之前的乘变成了加）。幂次也可以放到log的前面。

但是，可以发现如果按照这个loss去对$v(w)^t$或者$\theta^z$求偏导，在每一轮迭代的时候，只能够对词向量$v(w)^t$进行一次迭代。这里需要进行上下文窗口次的负采样才能对一个词的词向量进行迭代。显然，效率有些低。

在真正的word2vec实现的时候，需要变换一下思路：

$$\text {G}=\sum_{w^c \in \text {context}(w)} \sum_{u \in {w} \cup N E G(u)} p(u|w^c)$$

同样也是基于像CBOW一样的思想，已知上下文$(w^c)$的情况下，最大化中间词u。但是这里上下文$(w^c)$的每一个词都是独立的，不像CBOW是对上下文中所有的词向量进行累加。

下面重新看一下损失函数：

$$\text {Loss}=\sum_{w^c \in \text {Context}(w)} \sum_{u \in {w} \cup N E G(u)} L^{w}(u) * \log \left(\delta\left(v(w^c)^{T} \theta^{z}\right)\right)+\left(1-L^{w}(u)\right) * \log \left(1-\delta\left(v(w^c)^{T} \theta^{u}\right)\right)$$

这个log损失函数，如果我们忽略掉前半部分的累加。我们只看后面这部分。如果把上下文中的单个的词，变成了$w^x$的话，这一部分的损失函数与上一节讲过的GBOW的损失函数就一样了。也就是说每一次不是用所有上下文的累加和向量来进行梯度的学习。而是对每一个词单独学习梯度，并进行单独更新。实际上梯度形式也比较容易。只是比上一节求出来的多了一次累加。

1. Skip Gram训练主流程

• 对于中心词上下文词context(w)中的每一个词$w^c$，都需要选取一次负采样，也就是选取词w的正负样本，构造出正负样本；

• 计算loss对于theta以及$w^c$的偏导；($w^c$指的是我们举例的”我 是 中国”的”我” 或者”中国”)，计算偏导也是有顺序的，像CBOW首先更新loss对于$w^c$的偏导，因为这个偏导是最后我们需要更新词向量偏导的 1/n （n=负采样的数目 + 正样本 + 1）；

• 更新$w^c$对应的词向量；

skip gram与CBOW相比，每一次负采样skip gram只能更新一个词对应的词向量；而CBOW在一次负采样，可以更新n（n指窗口）个词。

1. 负采样的算法

假设词典（训练样本中所有的词）中有n个词，每一个词都会计算出一个长度，这个长度是一个0-1之间的长度，有的短，有的长，所有词的长度加起来的长度=1。

1、每一词的长度计算：

$$\operatorname{len}(\text {word})=\frac{(\text {counter }(\text {word}))^{\alpha}}{\sum_{w \in D}(\text {counter }(w))^{\alpha}}$$

分子：该单词在所有语料中出现的次数；幂次：相当于做了一个平缓；源码中这个平缓是3/4。

分母：语料中（字典中）所有词出现的次数的累加和。

显而易见这个长度是一个0-1之间的长度。而且所有的词的长度累加便是1。这样每一个词都有自己一个值域。比如说这里的w1（词1）可能是0-0.05，w2可能是0.05-0.11。每一个词的值域都是采用前开后闭的区间。

2、然后，初始一个非常大的数，源码中采用10^8，将0-1进行等分。然后每一段都会对应一个词（w1,w2,….,wn）的值域。

eg：比如这里的m1属于了w1,m2也属于了w1,但是m4和m5属于w2。

在每次进行负采样的过程中，会随机一个0-M之间的数，随机完数字之后，也就知道了随机的哪一个词。eg：随机到了1，那么m1就对应了词1（w1），那么也就是词1。如果我们随机到了4和5，那么m4和m5对应的是w2，那么就是词2是负样本。

注意：如果随机到的词和中心词相同，那么就跳过这次，再进行一次随机。